問題ＰＤＦ
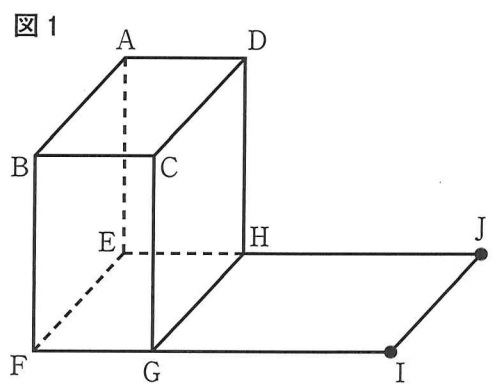
下の図１において、立体ＡＢＣＤ－ＥＦＧＨはＡＥ＝10ｃｍの直方体である。
辺ＦＧをＧの方向に延ばした直線上にある点をＩ、辺ＥＨをＨの方向に延ばした直線上にある点をＪとし、点Ｉと点Ｊを結んだ線分ＩＪは辺ＧＨに平行である。次の各問いに答えよ。

問１
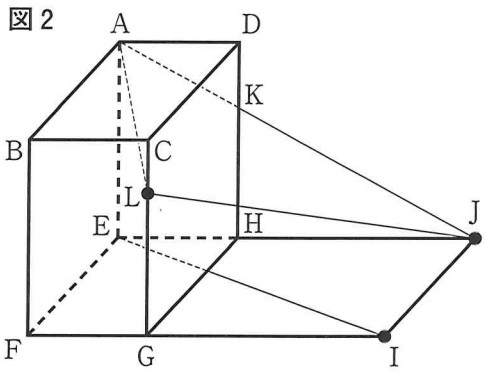
下の図２は、図１において、頂点Ａと点Ｊを結んだ線分ＡＪと辺ＤＨとの交点をＫ、辺ＣＧ上にある点をＬとし、頂点Ａと点Ｌ、点Ｊと点Ｌ、頂点Ｅと点Ｉをそれぞれ結んだ場合を表している。
ＡＢ＝10ｃｍ、ＥＩ＝16ｃｍ、ＣＬ＝ＤＫのとき、△ＡＪＬの面積は何ｃｍ²か。

問２
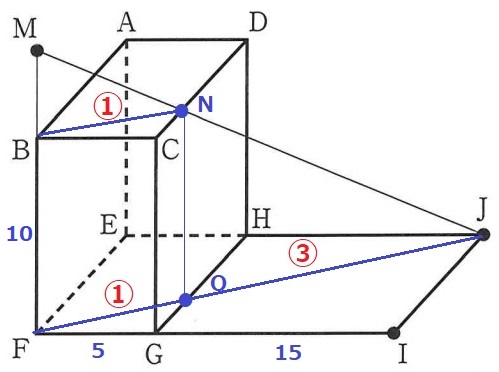
下の図３は、図１において、辺ＦＢをＢの方向に延ばした直線上にある点をＭとし、
点Ｊと点Ｍを結んだ直線ＪＭが辺ＣＤと交わる場合を表している。
ＡＢ＝10ｃｍ、ＥＨ＝５ｃｍ、ＧＩ＝15ｃｍのとき、線分ＦＭの長さは何ｃｍか。
ただし、答えだけでなく、答えを求める過程がわかるように、途中の式や計算なども書け。

問３
下の図４は、図１において、辺ＩＪ上にある点をＰとし、頂点Ａと頂点Ｃ、頂点Ａと点Ｐ、頂点Ｃと点Ｐ、頂点Ｅと頂点Ｇ、頂点Ｅと点Ｐ、頂点Ｇと点Ｐをそれぞれ結んだ場合を表している。
∠ＥＧＦ＝∠ＧＰＩ＝60°、ＢＣ＝ＩＰ＝５ｃｍのとき、立体Ｐ－ＡＣＧＥの体積は何ｃｍ³か。

＠解説＠
問１

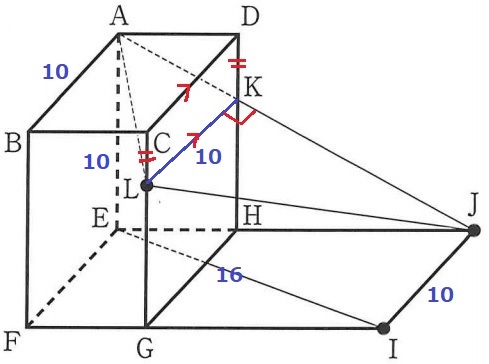
ＣＬ＝ＤＫより、ＬとＫは同じ高さにある。
ＣＤ//ＬＫ、ＬＫ＝10ｃｍ
面ＡＥＨＤ⊥面ＣＧＨＤ
→ＡＫは面ＡＥＨＤ上、ＬＫは面ＣＧＨＤ上の線分だからＡＫ⊥ＬＫ。

△ＡＪＬの高さはＬＫ＝10ｃｍなので、底辺ＡＪの長さが知りたい。

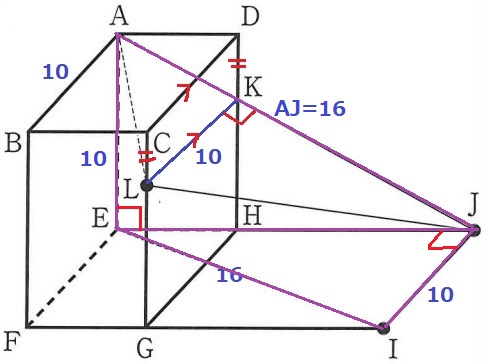
△ＡＥＪと△ＩＪＥに着目。
∠ＡＥＪ＝∠ＩＪＥ＝90°、ＡＥ＝ＩＪ＝10ｃｍ、共通辺ＥＪ。
２辺と間の角が等しく、△ＡＥＪ≡△ＩＪＥ。
ＡＪ＝ＩＥ＝16ｃｍ
したがって、△ＡＪＬの面積は、16×10÷２＝80ｃｍ²

問２

ＭＪはＣＤが交わるので、この交点をＮとする。
ＦＪとＧＨの交点をＯとおいて、図形全体を上から眺めると、
ＭＪとＦＪは重なり、面ＣＧＨＤ⊥面ＥＦＩＪだからＮの真下にＯがある。

ここで、△ＯＦＧ∽△ＪＦＩより、ＦＯ：ＯＪ＝ＦＧ：ＧＩ＝①：③
四角形ＢＦＯＮは２組の対辺が平行な平行四辺形（正確には長方形）で、ＢN＝ＦＯ＝①
△ＭＢＮ∽△ＭＦＪより、ＭＢ：ＭＦ＝ＢＮ：ＦＪ＝１：４
ＭＦ＝10×４/３＝40/３ｃｍ

＠＠
大雑把な流れだけ書きましたが、本問は説明問題なので、
直線や平面の位置関係を丁寧に記述すると骨が折れます(;´Д｀)
以下、公式解答を引用。

直方体の２つの側面が平行で、それを横切る平面との交線は平行になる。

問３

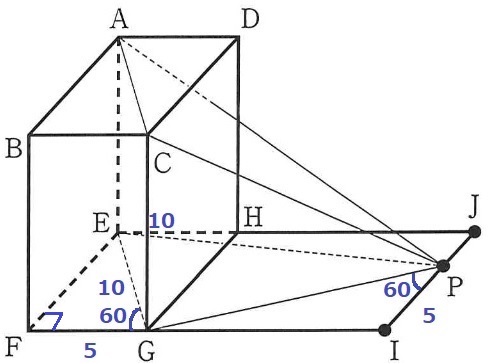
△ＥＦＧの内角は30°－60°－90°で辺の比は１：２：√３。
ＥＧ＝５×２＝10ｃｍ

底面ＡＥＧＣの面積は10×10＝100ｃｍ³
立体Ｐ－ＡＥＧＣの高さが知りたい。

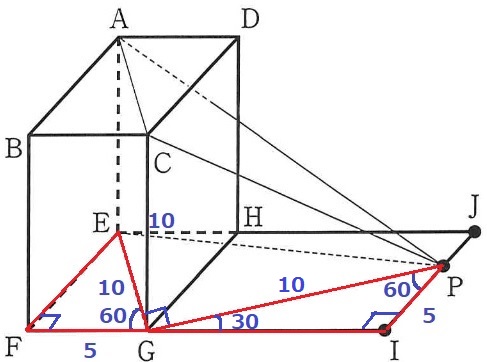
△ＧＩＰも１：２：√３の直角三角形で∠ＰＧＩ＝30°
ＰＧ＝５×２＝10ｃｍ
∠ＥＧＩ＝180－（60＋30）＝90°
立体Ｐ－ＡＥＧＣの高さはＰＧである。

したがって、体積は100×10÷３＝1000/３ｃｍ³
国私立高校入試解説ページに戻る