問題ＰＤＦ
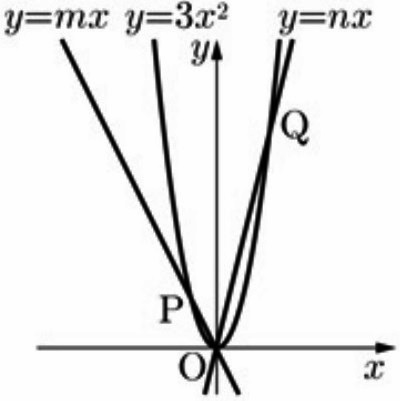
下の図のように、放物線ｙ＝３ｘ2と直線ｙ＝ｍｘ（ｍ＜０）、
直線ｙ＝ｎｘ（ｎ＞０）との交点のうち、原点Ｏと異なる点をそれぞれＰ、Ｑとする。
このとき、次の各問いに答えよ。
（１）
直線ＰＱの傾きｍ、ｎを用いて表せ。
（２）
点Ｐのｘ座標が－２、直線ＰＱの傾き－１のとき、ｎの値を求めよ。
（３）
整数ｍ、ｎを変化させたとき、傾きが10、切片が40以下の整数となるような
直線ＰＱは何本かくことができるか。
＠解説＠
（１）
Ｐはｙ＝３ｘ2とｙ＝ｍｘの交点。
３ｘ2＝ｍｘ
ｘ＝ｍ/３
これをｙ＝３ｘ2に代入→ｙ＝３×（ｍ/３）2＝ｍ2/３
Ｐ（ｍ/３、ｍ2/３）
同様にＱの座標を求めると、Ｑ（ｎ/３、ｎ2/３）←文字が変わるだけ。
傾きは（ｙの増加量）/（ｘの増加量）。
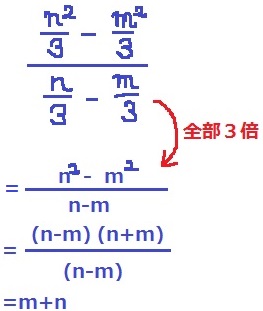
ＰＱの傾きは、ｍ＋ｎ。
（２）
Ｐのｘ座標は－２。
ｍ/３＝－２
ｍ＝－６
ＰＱの傾きは－１。
→前問より、ｍ＋ｎ＝－１
－６＋ｎ＝－１
ｎ＝５
（３）
初手がつかみにくい(;`ω´)
ｍとｎを変化させたとき、条件をクリアするｍとｎの組み合わせを模索する。
ポイントは『切片が40以下の整数』。
切片をｍ、ｎで表す。
ＰＱの傾きはｍ＋ｎなので、これをＰＱの式にあてはめると、
ｙ＝（ｍ＋ｎ）ｘ＋ｂ
これにＰ（ｍ/３、ｍ2/３）を代入。
ｍ2/３＝ｍ/３（ｍ＋ｎ）＋ｂ
ｂ＝ｍ2/３－ｍ2/３－ｍｎ/３
ｂ＝－ｍｎ/３≦40
ｍｎ≧－120
一方で、ＰＱの傾きは10なので、ｍ＋ｎ＝10でもある。
条件をまとめると…
ｍとｎは整数、ｍ＜０、ｎ＞０、ｍ＋ｎ＝10
ｍｎ≧－120、切片の－ｍｎ/３は整数
ｍとｎの組み合わせを絞っていく。
ｍ＝－１から当てはめ。
（ｍ、ｎ）＝（－１、11）（－２、12）（－３、13）（－４、14）
（－５、15）（－６、16）（－７、17）…
（－７、17）→－７×17＝－119でギリギリｍｎ≧－120だから、（－８、18）以降はなし！
さらに、切片－ｍｎ/３の値は整数でなければならないので、ｍかｎのいずれかに３の倍数が必要。
（ｍ、ｎ）＝（－２、12）（－３、13）（－５、15）（－６、16）
したがって、４本。
国私立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント