問題ＰＤＦ
図のように、長さが等しい棒を並べて、次の作業を行う。
〔作業Ⅰ〕正三角形を横一列につなげる。
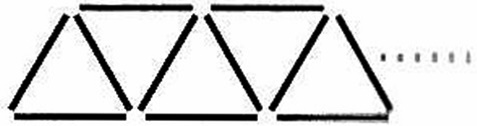
〔作業Ⅱ〕正方形と長方形を、正方形から始めて交互に横一列につなげる。
ただし、正方形は長方形にふくめないものとし、長方形の横の長さは縦の長さの２倍とする。
このとき、次の問いに答えなさい。
（１）
〔作業Ⅰ〕において、正三角形を200個つくるのに必要な棒の数を求めなさい。
（２）
〔作業Ⅱ〕において、700本の棒を並べて、最後に正方形をつなげて作業を終えた。
このとき、つくった正方形の数を求めなさい。
（３）
1930本の棒を並べて、〔作業Ⅰ〕〔作業Ⅱ〕をともに進めたところ、
〔作業Ⅰ〕でつくった正三角形の数と〔作業Ⅱ〕でつくった長方形の数の合計は295個だった。
このとき、つくった正三角形と長方形の数をそれぞれ求めなさい。
ただし、〔作業Ⅱ〕において、最後に長方形をつなげて作業を終えたものとする。
（１）
正三角形の個数に対応するように、棒をうまく分ける。
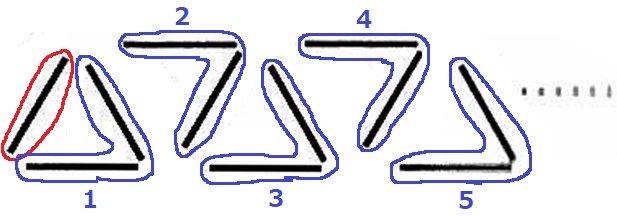
最初の１本だけを除外すると、正三角形の個数分だけ棒が２本ずつ追加される。
１＋２×200＝401本
（２）
正方形で終わった→正方形の右端の辺を周期の末端にして区切る。
最初の４本を除いて、700－４＝696本
１周期に棒は８本、正方形は１個。
696÷８＝87周期
最初の正方形を足して、その総数は88個。
（３）
連立方程式。
正三角形の個数をｘ個とすると、棒の本数は２ｘ＋１本。
長方形の個数をｙ個とする。
長方形で終わった→長方形の右端の辺を周期の末端とすると、棒の本数は８ｙ＋１本。
ｘ＋ｙ＝295 …①
（２ｘ＋１）＋（８ｙ＋１）＝1930
２ｘ＋８ｙ＝1928 …②
②－①×２をして、６ｙ＝1338
ｙ＝223
①に代入、ｘ＝295－223＝72
正三角形…72個、長方形…223個
国私立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント