人は完璧な存在ではないゆえ、ミスを0にすることは不可能である。
重要なのは、方法を工夫してミスをできる限り最小限に抑えること!
計算問題で歯がゆい思いをしている方へ、ここではミスを抑える方法を紹介します。
計算ミスの原因は一様ではないため、類型して挙げていきます。
数字は見やすい形で
きれいに書かなくても良いですが、見やすい数字を書くよう心がけましょう。
0を雑に書いて6としたり、筆算の桁ズレや小数点の位置ズレなど事故防止のためです。
少し大きめに書くことがポイント。
縦長より、やや横長を意識すると見やすくなります。
ノートを広く使う
ノートを隅々までビッシリ埋める人がいます。
スペースがもったいない気持ちはわかりますが、
広々と書いたほうが見やすくなり、ミスも少なくなります 。
分数は分母と分子を別の行に書く(あるいは行からはみ出てもよいので大きめに)
イコールの改行はゆとりをもって行うと見直しもしやすくなります。
無理しない
計算が苦手な子ほど暗算で処理しようしたり、式をすっ飛ばそうとする…。
正答率が高ければ暗算で良いですが、
そうでないならイコールのクッションは付けましょう。
「自分はミスを犯しがちだ!」と自認して、速さより丁寧さを心がけること!
4×5×6×7×8×9
=120×56×9 ←無理して一気にやらない。改行してワンクッションを置く。
=120×504
=60480
2(3X+2)+3(5X-3)
=6X+4+15X-9
=6X+15X+4-9 ←慣れないうちは同類項で整理。
=21X-5
イコールで繋げて縦長になってもいいので、途中をすっ飛ばさないようにしましょう。
『雑にやらない。急発進しそうであればブレーキを心がける』が肝心。事故防止!
速さの追求はちゃんとできるようになってからでも遅くありません。
計算方法を工夫する
効率の良い計算法はミス防止につながります。
1、 順序の入れ替え
30+31+32+33+34+35+36+37+38+39+40
(1の位が0になるように並び替え)
=(30+40)+(31+39)+(32+38)+(33+37)+(34+36)+35
=70+70+70+70+70+35
=70×5+35=350+35=385
2、切りの良い数字で調節
123-99
=123-(100-1)
=123-100+1
=23+1=24
398+197
=(400-2)+(200-3)
=600-5=595
3、分割や結合
35×18
=(7×5)×(9×2)=5×2×7×9=10×63=630
56×25=56×25×4÷4 ←×4÷4を加えても結果は変わらない。
=(56÷4)×(25×4) ←25×4=100を利用する。
=14×100=14000
4、分配法則
2×2×3.14+4×4×3.14
=4×3.14+16×3.14
=(4+16)×3.14 ←×3.14が共通。それ以外をカッコでくくる。
=20×3.14=62.8
99×77
=(100-1)×77 ←99=100-1を利用して分配法則で分割させる。
=100×77-1×77=7700-77=7623
4、因数分解の利用
153×147=(150-3)×(150+3) ←平方の公式
=22500-9 ←15×15は覚えておく(後述)
=22491
簡単にする=ミスを防ぐ。
倍数ルール
塾に通っている子はご存知かと思いますが、
倍数のルールを知っていると計算力が格段に上昇します。
約分、通分、整数の問題に効果テキメン。
2の倍数→ 偶数(1の位が0,2,4,6,8 )
3の倍数→ 各位の和が3の倍数
(123だったら、1+2+3=6 6は3の倍数なので123は3の倍数)
4の倍数→ 下2桁が4の倍数(628の下2桁は28で4の倍数、628も4の倍数)
5の倍数→ 1の位が0か5
6の倍数→ 2の倍数と3の倍数のルールを両方満たしている
(2の倍数×3の倍数=6の倍数のため)
8の倍数→ 下3桁が000か8の倍数
(6の倍数と違って、2と4の倍数ルールの複合ではないことに注意)
9の倍数→ 各位の和が9の倍数(3の倍数と構造が一緒)
10の倍数→ 1の位が0
25の倍数→ 下2桁が00、25、50、75
以上は必須事項といって良いでしょう。
7、8、11、13の倍数ルールもあるのですが使えにくいので覚えなくてOK。
結果を覚えておく
25×4=100 15×12=180 45×4=180
75×4=300 125×8=1000 (7×11×13=1001)
というように、結果を覚えていると倍数や約数を見つけやすくなります。
計算の経験を積んでいくと自然と覚えてきますので頑張りましょう!(ง `ω´)ง
(45×4=180は角度を思い出してみましょう。
45度の三角定規を4つ並べると1直線ですよね)
また、円の面積(半径×半径)や平方根の問題では、
2乗の結果(平方数)を暗記しておくと便利です。
1×1=1 2×2=4 3×3=9 4×4=16 5×5=25
6×6=36 7×7=49 8×8=64 9×9=81 10×10=100
11×11=121 12×12=144 13×13=169 14×14=196 15×15=225
16×16=256 17×17=289 18×18=324 19×19=361 20×20=400・・
中学入試では、3.14×2~9も覚えさせる塾もあります。
穴埋め計算
中学入試の難所、□に入るのは何でしょう計算。
ごちゃごちゃになるとミスが起きます。
いかにすっきりと簡潔にスマートに処理できるか。
つまづいてしまった場合は、大人が手順を見せて真似させてみましょう。
①→②→③の順です。
先に求めたいところを線で囲って、全神経をそこに注ぎ込みます。
①の2×3=6は、×(かける)の前の求め方を忘れたとき用です。
□×3=6で、□を求めたいときは6÷3=□と割り算を使えばいいとわかりますよね。
なるべく割り算は横線1本で処理。見やすいからです。
②は35/10を1つ目の式で約分しました。
3.5を頭の中で約分できる人は、そのまま7/2と記入です。
③で一度、式を整理。通分で分母は28だとわかりやすい。
ごちゃごちゃ書かない。整理する方法を大人が見せて伝授する!
見直し
計算が終わったら、答えを見る前に軽く見直しをしましょう。
方程式の問題では計算結果を元の問題文に代入することで、
事後的に正誤を確認することができますよね。
およそ計算(概算)も見直しの有効手段です。
およそ計算とは例えば28×58の場合、28は30弱、58は60弱ですので、
28×58=30弱×60弱=1800弱だろう、と
頭の中でおよその値を推測する計算です。
詳しい正誤の判定を調べられませんが、
ケタ違いを起こしやすい小数の計算ではミスを防げます。
7.2×9.12ならば63ちょいですから、
6.5664とか656.64は誤りとすぐわかります。
計算過程は残しておく
計算が苦手な子ほど、答えを間違えたときに全て消してしまう傾向があるように思えます。
これではどこで何を間違えたのかがわからず、失敗を活かせません。
間違えても計算過程は全て保存し、どこを間違えたのかを精査してみて下さい。
計算方法そのものを間違えている場合、自分の悪いクセを早期に見抜くことが何よりも大事。
間違えたところを見つけたら、隣の空きペースで再挑戦です(ง `ω´)ง
筆算も書くようにしましょう(筆算も計算が苦手な子ほど消してるような気がする)
どの式で用いたかわかるように計算式の近くに書きとめ、
答えが間違ったときに筆算も見るよう心がけてください。
地道な努力が計算力をUPさせる秘訣。
受験生が間違えやすい代表例を挙げます。
例1)負の数で符号ミス
2-6×(-2)
=2-12
=-10
典型的な符号ミス!
マイナスとマイナスはプラスになる。
正解は、2-6×(-2)=2+12=14
例2)式の展開で符号ミス
2(2X+3)-3(5X-4)
=4X+6-15X-12
=-11X-6
先と似た代表的なミス。
-3のマイナスは-4にもかかるので符号が+に変わります。
答えは、-11X+18
例3)片方の分子のみで分母を約分
(4X+6)/8=(2X+6)/4
/(スラッシュ)は、÷と一緒で分数の線と同じです。
上の式は分子の4Xと分母の8を約分していますが、
8は+6にもかかるので4Xだけで約分はできません。
分子が多項式(項が複数ある)の場合は、全ての項にかかる約分しか行えません。
片方だけの約分は禁物です。
正解は、(4X+6)/8=(2X+3)/4
例4)逆数のミス
分数の割り算は逆数(分母分子をひっくり返した数)をかけますが、
その逆数を間違えるミス。
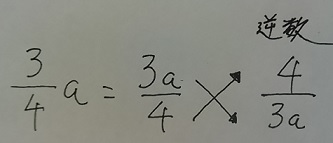
例えば、3/4・aのaは、もともと分子にありますから(3a)/4なので、
その逆数は4/(3a)となり、分母に移ります。
aを分数で示せば、a/1ですから、逆数は1/aですよね!
例5)乗数の取扱い
(-2)4と-24
(-2)4=(-2)×(-2)×(-2)×(-2)=16
-24は、-に指数がかかりませんから、-2×2×2×2=-16
カッコがついて負の数の累乗が偶数回→+、奇数回→-。カッコがないと-。
例6)指数法則
a2×a3=a6
掛け算なので、2乗×3乗=6乗としたいところですが、
a2=a×aとa3=a×a×aをかけると、a×a×a×a×a、つまりa5になります。
(a2)3となると、(a×a)×(a×a)×(a×a)=a6になります。
自信のない方は指数法則を確認して下さい。
例7)代入時にカッコを忘れて符号ミス
x=-2のとき、-x+x3の値を求めよ。
-2+-23=-2-8=-10
マイナスや乗数を代入するときはカッコでくくらないと符号ミスが起きます。
正しくは、-x+x3= -(-2)+(-2)3=2-8=-6
連立方程式で代入法を用いるときも注意が必要です。
例8)移項の符号ミス
移項するとプラスマイナスが逆に変わります。符号の入れ替えに注意です。
移項していないものも変えてしまうミスも見たことがあります。
例9)文字式と方程式の計算を混同する
〔3x+5-3x-2〕と〔3x+5=-3x-2〕は全く異なる問題です。
方程式を習ったあとに文字式に戻ると、
式の途中に無理やり=を入れ、方程式で解く子がいました。
例10)方程式の最後
3/4x=12
x=12×3/4=9
上は3/4をかけていますが、正しくは割り算です。
計算が苦手な子が間違えやすいところでした。
正しくは、x=12÷3/4=12×4/3=16
他にもいろいろなミスのパターンがありますが、あげるとキリがないのでこの辺で。
とくに因数分解や平方根はいままでの計算とは方法が異なりますから、独特なミスを犯しがち。
計算ミスというのは、だいたい同じところでミスをする場合が多いです。
自分がどこで落ちやすいのかを早めに見つけてください。
そのために、間違えたからといって計算過程をすぐ消してはいけません。
正しい方法で反復練習を
計算には各々にクセが見受けられます。
その方法に独特の悪いクセがあるとき、その是正は容易くありません。
まずは早期に落としやすいポイントを見つけること。そして、正しい方向へ徐々にずらしていきます。
空いてるスペースに 模範解答通りの計算式をそのまま書いてみましょう。
(学ぶことは真似ること!自己流のアレンジなんて二の次だわ!)
どこでどう間違えたのか、どうすれば間違いにくいのかを考えます。
目立つように枠で囲ったり、色ペンやマーカーで際立たせるのもGOOD。
問題は定着。
正しい模範解答をせっかくノートに書いても、一度書いたら満足してノートを見なくなる人がいます。
翌朝、三日後、一週間後、復習をしないまま時が経過するとふたたび悪い癖がぶり返している…。
これはとても多かったです。
一度、正しいやり方を吸収しても忘れてしまうと本番では意味なし!
模範解答を何度も眺め、慣れるまでそれを真似る。類題を解く!
(もう一度いう、学ぶことは真似るということ!!)
過去に解いた問題をもう一度繰り返すのはダルく感じると思いますが、
それが復習するということです。復習をあなどってはいけません。
重要!↓
正しい知識や方法を頭にいれること!
間違ったものを頭にいれると、なかなか抜け出せなくなる。
計算力の上達
暗算
暗算って脳の体操に良いらしいです。
暗算をすると頭の瞬発力や回転力も速くなります。頭の忍耐力もUP!
(柔道のヤワラちゃんも暗算をしながら組み手の練習をしていたのだとか・・。相手の重心を絶えず崩しながらとっさの判断でベストなワザを繰り出す柔術には、頭の回転力が必要らしい…)
100マス計算や1000から13を引き続けるだけでもよいので、続けることがポイントです。
なるべく小さい頃から始めるのが良いですね٩( ‘ω’ )و
今や世界をまたにかける公文式でも、計算力は重視しています。
必ずしもというわけではなさそうですが、珠算を習っていた子は暗算が得意な子が多いと聞きます。
珠算には計算を得意とするヒントが隠されているのかもしれませんね。
車のナンバープレート
個人的にオススメ。
ナンバープレートの4桁をうまく利用して、答えが10になる計算式を組み立てます。
例えば、7316だったら・・
6÷3+7+1=10 (7+6-3)×1=10
対向車が通り過ぎるまでに組み立てられたらGOOD JOB!
複数の解法を編み出せればFINE PLAY!
単に計算するのではなく、自ら計算式を立てなくてはならないので、
未知の解法を手探りで探しあてるところがミソです。
9270はどうでしょうか?
一見不可能に思われますが、
9+2-70(7の0乗)=9+2-1=10
0乗は1になります。(ただし、0の0乗を除く)
10も20も100000も全て1です。0がきたときの伝家の宝刀。
〔1・2・3・4〕の4つの数字をもとに四則計算と( )のみの演算で、
0~25を作ることもできますよ!
4-3+1-2=0 … (2+3-4)×1=1 …
やってみましょう。
時間を計測する
計算に慣れてきたら、時間を意識しましょう。
計算ドリルによっては目安のタイムが設定されています。参考にしてみてください。
ストップウオッチで計れば、本番さながらの緊張感を演出することもできます。
サボは〔しゃべるストップウォッチ〕という無料アプリを使っています。
カウントダウンや〇秒おきに『ピッ』と鳴らせます。
ダラけやすい自室での勉強に刺激を添えることもできます。
受験の世界では時間の概念は重要!
制限時間があるなかでケアミスを出さないよう、緊張に慣れさせる。
高い正答率を維持しながらベストレコードをたたき出せれば計算の上級者ですね(^^)
ソフトを利用する
最近では、計算力を高めるためのゲームソフトが売られているようです。任天堂DSを持っている方はベネッセが出している「数センス計算力UPトレーニングすうトレ」が面白そうです。

希望小売価格:3990円なり。中古だともっと安く買えるかも。。
大小センスや概数センスの問題は数字に対する感覚を養えます。
数学者のピーター・フランクルさんも算数には数的センスが大切だと仰られていました。
ほかにも、良いソフトがあるかな?無料でできるものが良いですよね(´Д`)
計算ではないですが、花まるラボさんが出している『Think!Think!』というアプリががお勧めです。
花まるサボさんのページ
能力開発系のアプリでは無料とは思えないほどのクオリティの高さ。
組み合わされたキューブが穴を通るか。
マウスのロボットを動かして立体迷路を攻略する。
立体図形の切断面を考えるなどなど、デジタル教材ならではの教材が目白押しで、
幼児から遊べます。
対応はiPhone、iPad、iPod touch。スマホでもできますが、
タブレットの方がプレイしやすいですね。
教育系アプリはやはりタブレットが一番使いやすいです。
勉強方法の紹介に戻る




コメント