2016年度　横浜翠嵐高校・特色検査【課題２】問題解説

〔科学者の心構えに関するリード文〕
◆設問１
ビュリダンのロバの説明文と、それに近い例を選択する。
すべて英語が書かれている。
英文のレベルは難解ではないが、文章が長いので時間との勝負。

＠ビュリダンのロバ＠
自分に近い方を選ぶと決めていたロバが食べ物を探していたところ、
自分の左側と右側に干草があり、両者とも自分から等距離にあった。
ロバがどちらの干草を食べようか決めかねてたら、とうとう餓死してしまった。
理論を強調しすぎるとかえって良くない。ときにはそれを覆す自由意志が必要だと説く逸話。

◆設問２
下線部２「正五角形のような対称性」とあるが、今、机の表面に正五角形がかかれている。さらに正五角形の中心に点Ｏがかかれており、５つの頂点付近には反時計回りで①～⑤の番号が振られている（図１）。また、この正五角形と合同な形の板があり、両面の頂点付近には１～５の番号が、表と裏で同じになるようにかかれている（図２）。

図１の正五角形の上に、図２の板をぴったりと重ねる。板と板にかかれた頂点の番号が一致している状態（これを「初期状態」と呼ぶことにする）から、Ｏを中心として板を反時計回りに72°回転すると、頂点１、２、３、４、５はそれぞれ②、③、④、⑤、①の位置に移動してぴったりと重なる（図３）。また、初期状態から、①とＯを通る直線を軸として板を裏返すと、頂点１、２、３、４、５はそれぞれ①、⑤、④、③、②の位置に移動してぴったりと重なる（図４）。このように、回転や裏返し、およびそれらの繰り返しで、元の図形とぴったり重なる性質のことを正五角形の対称性という。各問いに答えなさい。

問１
板を机の正五角形にぴったりと重ねるとき、頂点①～⑤と、頂点１～５の対応は何通りあるか。
ただし、初期状態も１通りに数えること。
10通り
*時計回りにまわして５通り。
裏にし、同様にまわして５通り。計10通り。

問２
頂点①～⑤から異なる２点を選んでＡ，Ｂとする。初期状態から直線ＯＡを軸として板を裏返し、引き続き直線ＯＢを軸として板を裏返す。この結果、板は初期状態と比べて、Ｏを中心としてＡからＢの方向に２×∠ＡＯＢだけ回転している。なぜそうなるか説明しなさい。
必要ならば、図や数式を用いて説明してよい。
解説参照
*まずは内容理解。
５つの頂点から２つ選び、Ａ、Ｂとする。
Ａと中心Ｏを軸にひっくり返し、ＢとＯを軸にひっくり返すと、
初期状態からＡからＢ方向に２×∠ＡＯＢだけ回転しているという。

↑確かに・・。
図と数式を使うとしても、どうやって説明すればよいのやら(‘ω’)怒

Ａはわかりやすいように１に固定してみる。
（正五角形は回転させても互いの位置関係は変わらないので、Ａが１以外でも同じだから）
初期状態では番号が反時計回りに振られているが、１度裏返すと時計回りとなり、
再び裏返すと反時計回りに戻る。
並び方の向きが同じになるため、初期状態の正五角形を回転させたのと同義となる。
１回目の裏返しではＡの位置にある１は変わらない。
２回目の裏返しでは、ＢＯを対称の軸として１が反対側にうつる。
反対側に移動したＡをＡ’とおくと、Ａ（１）～ＢＯ（対称の軸）とＢＯ～Ａ’（１）の角度が等しいので、
『ＡからＢの方向に２×∠ＡＯＢだけ回転している』。

こんな感じかな（＾＾;
対称移動させると対応する点から対称の軸までの距離がそれぞれ等しくなり、
本問は距離ではなく、角度になった感じです。
回転させたときにもとの図形をぴったり重なることを回転対称といい、
対称移動（裏返し）を回転移動に見立て、正五角形の回転対称の特徴を活かした設問なんだと思う。

◆設問３
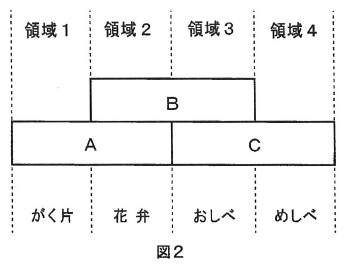
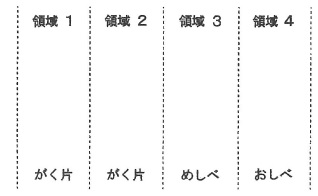
下線部３「この遺伝子を突きとめられれば、花の形を決める普遍的な法則が見つかる」とあるが、被子植物の花の各部分の形を決めている遺伝子と、それらによる調節のしくみについて、シロイヌナズナを用いた研究をもとに、1991年にコーエンとマイロヴィッツにより「ＡＢＣモデル」が提唱された。花を同心円状に４つの領域に分け、各領域を外側から領域１～４とすると、領域１にはがく片、領域２には花弁、領域３にはおしべ、領域４にはめしべが形成される（図１）。

これらの花の器官の形成を調節する遺伝子Ａ、Ｂ、Ｃが存在し、遺伝子Ａは領域１と２で、遺伝子Ｂは領域２と３で、遺伝子Ｃは領域３と４ではたらく。遺伝子Ａでがく片が、遺伝子Ａと遺伝子Ｂで花弁が、遺伝子Ｂと遺伝子Ｃでおしべが、遺伝子Ｃでめしべが、それぞれ形成される（図２）。

このモデルでは、遺伝子Ａが失われると遺伝子Ｃが領域１と２でもはたらくようになり、遺伝子Ｃが失われると遺伝子Ａが領域３と４でもはたらくようになるとしている。同種の植物に一重咲きのものと八重咲きのものがみられるといった花の形態変化は、特定の遺伝子のはたらきが失われることにより生じたと考えられている。次の各問いに答えなさい。

問１
次に述べる（１）～（３）の場合について、領域２に形成される花の器官をそれぞれ書きなさい。
（１）遺伝子Ａが失われた場合。
（２）遺伝子Ｂが失われた場合。
（３）遺伝子Ａと遺伝子Ｂの両方が失われた場合。
（１）おしべ（２）がく片（３）めしべ
*ＡＢＣモデルの内容理解。
Ａ→がく片、Ａ＋Ｂ→花弁、Ｂ＋Ｃ→おしべ、Ｃ→めしべ
（１）Ａを失うところにＣが発現。Ｂ＋Ｃになり、おしべ。
（２）Ｂを失うとＡだけになり、がく片
（３）ＡとＢがなくなると全ての領域でＣのみ→めしべ
めしべだけの花とは、興味深いですね((( ;ﾟдﾟ))

問２
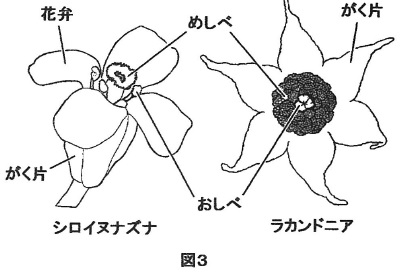
メキシコに自生するラカンドニアという植物の花は、外側から、領域１と領域２ではがく片が、領域３と領域４では、シロイヌナズナと比べて花の器官の形成位置が逆転しており、それぞれめしべ、おしべが形成される（図３）。これは、遺伝子Ａ、Ｂ、Ｃのはたらく領域がシロイヌナズナとは異なるためであると考えられている。ラカンドニアではどの遺伝子がどの領域ではたらいていると考えられるか。図２にならって遺伝子Ａ～Ｃがどの領域ではたらくかを図示しなさい。

*解答↓

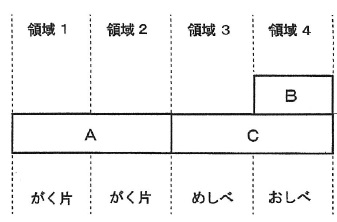
先ほどと同様。
Ａ→がく片、Ａ＋Ｂ→花弁、Ｂ＋Ｃ→おしべ、Ｃ→めしべ
ここはとりやすかったと思う。

◆設問４
下線部４「実験データは必ず誤差を含んでいるので、この誤差以上に桁数を増やして記しても全く意味がない。このように意味のある桁数以下を切り捨てた結果を『有効数字』と呼ぶ」とあるが、実験データは記されている数の最後の桁に誤差を含んでいる。たとえば、下図のようにサクラの花に１ｃｍきざみの目盛りのものさしを当てて大きさを測るとき、2.4ｃｍと読み取れるが、「４」が誤差を含むのである。

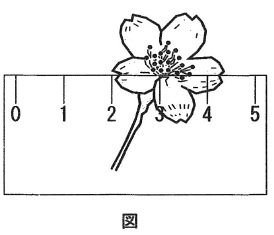
下記の【測定値】には、ある地点ＡＢ間の直線距離を４つの区間に分けて測定した値が記載されている。これらは、それぞれ最後の桁に誤差を含んでいるものとする。これらの値を合計し、地点ＡＢ間の距離を正しい有効数字で答えなさい。
このとき、答の数値について、誤差を含む桁の数字に下線を引くこと。
《　例　》　<測定値>15ｍ　11ｍ　<答>26ｍ
【測定値】　21.2ｍ　1.358ｍ　117ｍ　4.47ｍ
１４４ｍ
*21.2＋1.358＋117＋4.47＝144.028ｍ
４つの数字のなかで、117ｍは一の位の７に誤差を含んでいる。
つまり、一の位に誤差があるので一の位に下線を引き、
小数点以下は有意性（統計的に意味をもつ）のない値として除外する。

◆設問５
本文を要約した英文において、空欄部分をimportantを含む15語以内の英語で埋める。
難問特色検査の解説ページに戻る