2017年度　希望ヶ丘高校【課題３・４】問題解説

【課題３】
〔A〕
この春から新たに委員会活動を行う生徒、Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆの６人は、
それぞれ決まった曜日に活動する予定である。
委員会室に６人の机を用意しなければならないが、用意できる机は４つしかない。
それぞれが活動する曜日と、６人の使用する机を決める条件は次のとおりである。

<委員会活動を行う曜日>
Ａ：木　　Ｂ：月・水・金　　Ｃ：木・金　　Ｄ：火・木　　Ｅ：月・火　　Ｆ：火・木・金
<条件>
・６人はそれぞれ毎週、決まった曜日に活動し、決まった机を使用する。
・活動部が重なっていない人どうしで１つの机を共有することができる。
・１つの机を３人以上で共有することはできない。

◆設問１
人と机をどのように組みあわせても、他の人と共有することなく１人で使うことになる生徒が１人いる。
それは、ＡからＦまでのうち誰か。
Ｆ
*６人と４つの机をどのように組み合わせても、誰とも共有しない者を選ぶ。
論理問題は条件を的確かつ素早く理解すること！
糸口をみつけるために情報整理を行う。

曜日ごとに活動する人物を一覧で表示する。
木曜日は４人が活動するので、それぞれの机に１～４の番号をふし、
ＡＣＤＦに１・２・３・４の机を振り分ける。
同じ人物は同じ机を使うので、木曜以外も書き込む。

すると、ＢとＥが残り、金曜からＢは１か３、火曜からＥは１か２となる。
Ｂ・Ｅは不確定だが、いずれにせよ、４番の机はＦが独占することになる。
よって、答えはＦ。

◆設問２
設問１で答えた人以外のある人が「１人で机を使いたい」と申し出た。
しかし、そのある人が１人で机を使うこととすると、机が足りなくなってしまう。
ある人とはAからFまでのうち誰か。考えられる人すべてを答えなさい。
Ｂ・Ｅ
*上の図をみれば、おわかり頂けるかと。
ＡＣＤＦにそれぞれ１・２・３・４の机を割り当てたが、
机の番号が２３４１でも３４１２でも３１２４でもＡＣＤＦ間では机がかぶらない。
しかし、ＢかＥが「１人で机を使いたい」とゴネてきたら、
上の図のように誰かとかぶるおそれがでてくる。

〔B〕
陸上競技大会でＡ、Ｂ、Ｃ、Ｄ、Ｅの５人で100ｍ走をした結果について、各人が次のような発言をしている。
それぞれが自分の順位または他人の順位のうち、一方だけ本当のことを言い、他方はうそを言ったとすると５人の正しい順位はどうなるか。
１着から順に答えなさい。ただし、同順位はなかったものとする。
Ａ：私は２着で、Ｄは５着だった。
Ｂ：私は５着で、Ｃは２着だった。
Ｃ：私は２着で、Ａは４着だった。
Ｄ：私は４着で、Ｂは１着だった。
Ｅ：私は４着で、Ｃは１着だった。
ＢＣＡＥＤ
*これも最初の取っ掛かりをつかむのが難しい。
地道に背理法みたいな方法がよいと思う。
Ａの発言で『私は２着』と『Ｄは５着』のうち、どちらかが本当で、他方が嘘だから、
仮に『私は２着』が本当と仮定して考える。
すると、Ａが２着で、Ｄは５着ではない。
Ａが２着だから、Ｂの発言では『Ｃが２着』が嘘で、『私は５着』が本当になる。
しかし、Ｃの発言『私は２着』はＡが２着なので嘘となるが、
『Ａは４着』はＡが２着であることから双方が嘘となり、矛盾が生じる。
矛盾が生じた原因は、Ａの発言『私は２着』が本当だと仮定した前提が誤りだから。
よって、Ａの発言は『Ｄは５着』が本当で、Ａは２着ではない。
あとはドミノ倒しのようにすべての順位がうまる。

◆設問１
銀貨１枚と等しい価値を持つのは銅貨何枚か、答えなさい。
２００枚
*連比。
金　：　銀　：　銅
１　：　　　　　2500
２　：　２５
２　：　２５　：5000

銀貨２５枚に対して銅貨は５０００枚なので、
５０００÷２５＝２００枚

◆設問２
薬草屋で、薬草を１束買った。薬草１束の値段は、銅貨７０枚である。
金貨１枚を支払うと、お釣りはいくらになるか。銀貨と銅貨の枚数で答えなさい。
ただし、銅貨の枚数が最も少なくなるようにすること。
銀貨―１２枚、銅貨―３０枚
*前問より、金貨：銅貨＝２：５０００＝１：２５００
問題文の金貨１枚を『銅貨２５００枚で支払うと』に置き換えればわかりやすい。
お釣りは、銅貨で２５００－７０＝２４３０枚分。
銀貨１枚＝銅貨２００枚だから、
２４３０÷２００＝１２・・３０
銀貨１２枚、銅貨３０枚

◆設問３
金貨１枚を持って、薬草屋、帽子屋、靴屋、鎧屋へ買い物に出かけた。
薬草１束の値段は銅貨７０枚、帽子１個の値段は銅貨３００枚、
靴１足の値段は銅貨４５０枚、鎧１領の値段は銅貨１６００枚である。*領は鎧を数えるときの単位
この４軒の店のうち３軒の店に立ち寄りここにあげた商品を買ったところ、
最終的に手元に銀貨４枚と銅貨１６０枚が残った。
どの商品をいくつ買ったか、それぞれ求めなさい。
なお、立ち寄らなかった店の商品については、解答欄に０と答えなさい。
薬草―７束、帽子―２個、靴―１足、鎧―０領
*これも銅貨を基準に考える。
金貨１枚＝２５００枚。
手元には、２００×４＋１６０＝９６０枚分の銅貨が残った。
支払った銅貨は、２５００－９６０＝１５４０枚。
この時点で鎧１領未満なので、立ち寄らなかった店は鎧屋。
残りの３店で少なくとも１つずつは買ったので、
１５４０－（７０＋３００＋４５０）＝７２０枚。

残り７２０枚の銅貨でキリよく〈薬草７０枚、帽子３００枚、靴４５０枚〉を買う組み合わせを考える。
２番目に高い靴をもう１足買うと、７２０－４５０＝２７０枚
帽子は買えない。また、２７０は７０の倍数ではないので、薬草もキリよく買えない。
よって、靴は１足のみとなる。

残り７２０枚の銅貨でキリよく〈薬草７０枚、帽子３００枚〉を買う組み合わせを考える。
帽子を１個買うと、残り７２０－３００＝４２０枚
４２０枚は７０の倍数で薬草６束分。
以上をまとめると、薬草７束、帽子２個、靴１足、鎧０領。
値段が最も高い品物の個数を増やし、
残りの金額が最も安い薬草の値段で割り切れるかを調べていく。

〔B〕
球がひとつも入っていない袋Ｘと袋Ｙを用意し、次の操作にしたがって球を入れる。
また、最初の操作を１回目として、以後操作のたびに２回目、３回目と回数を数えることにする。
操作は、操作Ａ、操作Ｂのどちらかである。

操作Ａ：その回の回数と同じ個数だけ、球を袋Ｘに入れる。
操作Ｂ：その回の回数と同じ個数だけ、球を袋Ｙに入れる。

また、操作を繰り返し、どちらかの袋に球が１０個以上入った時点で操作を打ち切る。
例を参考にしてあとの各設問に答えなさい。

例
１回目　操作Ａを行う、袋Ｘに１個の球が入り、
それぞれの袋の球の個数は、袋Xに１個、袋Ｙに０個となる
２回目　操作Ｂを行う。袋Ｙに２個の球が入り、
それぞれの袋の球の個数は、袋Xに１個、袋Ｙに２個となる。
３回目　操作Ａを行う。袋Ｘに３個の球が入り、
それぞれの袋の球の個数は、袋Xに４個、袋Ｙに２個となる。
４回目　操作Ａを行う。袋Ｘに４個の球が入り、
それぞれの袋の球の個数は、袋Xに８個、袋Ｙに２個となる。
５回目　操作Ａを行う。袋Ｘに５個の球が入り、
それぞれの袋の球の個数は、袋Xに13個、袋Ｙに２個となる。
袋Xの球が10個以上になったため、この時点で操作を打ち切る。
この連続する操作をＡＢＡＡＡと表すことにする。

◆設問１
連続する５回の操作ＢＡＢＡＡのあとに、袋Ｘ、Ｙに入っている球の個数を答えなさい。
Ｘ―１１個、Ｙ―４個
*ルールの確認。
AはX、BはYに置き換えたほうがいいかも。
ＢＡＢＡＡは、ＹＸＹＸＸ。
X：２＋４＋５＝１１個
Y：１＋３＝４個

◆設問２
最も少ない回数で操作を打ち切るとき、何回目の操作まで行うことになるか。
４回目
*ＸかＹのどちらかがストレートに続けば、
１＋２＋３＋４＝１０個で操作打ち切り。

◆操作３
袋Ｘ、Ｙを一度空にして新たに操作を行った。
操作を打ち切ったとき、球は袋Ｘに１３個、袋Ｙに８個入っていた。
操作を打ち切るひとつ前の回で、袋Ｘと袋Ｙに入っていた球の個数を答えなさい。
Ｘ―７個、Ｙ―８個
*ＸとＹの合計は１３＋８＝２１個。
２１＝１＋２＋３＋４＋５＋６なので、６回目で操作が打ち切られた。
Ｘが１０個以上だから、５回目はＸに１３－６＝７個、Ｙに８個入っていたことになる。

◆設問４
袋Ｘ、Ｙを一度空にして新たに連続する操作を行った。
６回目の操作で袋Ｘに１０個以上、Ｙには９個の球が入ったので操作を打ち切った。
しかし、５回目までのいずれかの回の回数で、球を入れ忘れて（１個も球を入れないまま）
次の回の操作をしてしまったことに気が付いた。
この結果となる連続する操作として考えられるものをすべて答えなさい。
ただし、入れ忘れは１回のみとする。
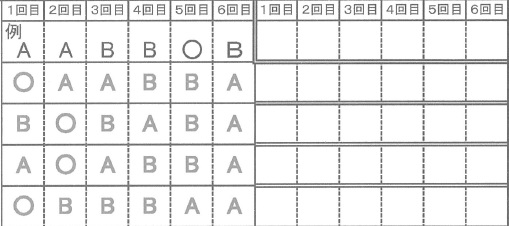
答えは解答欄にある例にならってＡとＢを用い、球を入れなかった回は〇で示すこと。
解答欄の例は、５回目に球を入れず、６回目で操作で打ち切った場合を示している。
また、解答欄の例は記入例であり、この設問の条件を満たしていない。
また、解答欄はすべて埋まるとは限らない。
←答え
*Ｘが１０個以上なので、６回目はＸに球がはいる。
Ｙの９個は確実なので、５回目までに９をどうつくるかを考える。
５回目なので、１～５の整数。同じ整数は使えない。
<４・５>
<１・３・５>　←４を１・３に崩す。
<２・３・４>　←５を２・３に崩す。
この３通りしかない。

Ｙ<４・５>
Ｘ<１・２・３>
１回目、２回目、３回目のなかで球を入れなかった回はどれかを考える。
６回目の６個の球を含めて、Ｘは１０個以上でなくてはならない ので、
３回目でＸに球を入れないと、１＋２＋６＝９個になってしまう。
ということは、１回目か２回目に球を入れなければ、Ｘは６回目に１０個以上となる。
１―○  ２―Ｘ　３―Ｘ　４―Ｙ　５―Ｙ　６―Ｘ
１―Ｘ　 ２―○　３―Ｘ　４―Ｙ　５―Ｙ　６―Ｘ

Ｙ<１・３・５>
Ｘ<２・４>
６回目の球を含めて、６＋４＝１０しかないから、２回目に球を入れない。
１―Ｙ　２―○　３―Ｙ　４―Ｘ　５―Ｙ　６―Ｘ

Ｙ<２・３・４>
Ｘ<１・５>
６回目の球を含め、５＋６＝１１しかないから、１回目に球を入れない。
１―○　２―Ｙ　３―Ｙ　４―Ｙ　５―Ｘ　６―Ｘ

以上、４通り。操作名を記入するので、ＸをＡ、ＹをＢに置き換えること！
難問特色検査の解説ページに戻る