2017年度　平塚江南高校・特色検査【課題２】問題解説

次の‹資料１›‹資料２›を読んで、後の問いに答えなさい。
‹資料１›
日本の発電電力量の推移を大まかに見ると、1962年度では火力発電と水力発電がほぼ同じであるが、2012年度になると圧倒的に火力発電が大きな割合を占めるようになった。

さらに、下の円グラフのように、日本の家庭で使うエネルギーのうち、電気エネルギーが占める割合は、かつては４分の１未満であったが、近年ではおよそ半分を占めるようになっている。

‹資料２›
電気エネルギーを光に変える方法には、いくつかの種類がある。
19世紀の後半に発明された白熱電球は、ろうそくや油を用いたランプに比べて、取り扱いが簡単で強い光が得られるため、発電・送電システムの整備にともなって20世紀の初頭には広く普及した。
しかし、白熱電球は、電気エネルギーの大部分を熱エネルギーに変換してしまうので、光エネルギーへの変換効率はおよそ８％から１５％といわれている。
それに対し、現代では、白熱電球と比較して、熱の発生が少なく、エネルギーの変換効率のよい蛍光灯やＬＥＤ（発光ダイオード）電球が、次第に用いられるようになってきている。

問１
1980年度以降の発電電力量の推移は次の表のとおりであり。
表中のア～エの空欄に入る語を選びなさい。
①火力　②水力　③原子力　④太陽光
ア：②　イ：①　ウ：③　エ：④
*資料１の折れ線を見てもよいが、見なくても解けるようにしておきたい。
2012年で桁違いの発電電力量を誇るイが火力。
2010～12年にかけて激減したウは電子力。
理由は2011年の東日本大震災（福島第一原発事故）。
発電電力量がさほど変わらないアは水力。もっとも少ないのが太陽光。

問２
‹資料１›の円グラフより、1973年度における１世帯あたりの電気エネルギーの消費量は、

の計算から、およそ８４憶Ｊであったことがわかる。
2014年度の1世帯あたりの電気エネルギーの消費量は、1965年度の1世帯あたりの電気エネルギーの消費量はおよそ何倍か。小数点第２位を四捨五入して、小数点以下第１位まで答えよ。

4.4倍
*計算式は立てやすいが面倒くさい(´Д｀)
2014年；340×51/100＝173.4
1965年；170×23/100＝39.1
173.4÷39.1＝4.43…　→　4.4倍

問３
電気エネルギーが一般家庭で広く利用される理由として誤っているものを選びなさい。
①熱・光・動力などの別の形のエネルギーに変換しやすい。
②送電線を整備することにより、個別の家庭に継続的に送ることができる。
③情報を伝達することや、記録することにも利用できる。
④余った電力を、家庭でもほとんど無限に貯蔵することができる。
④
*④：「ほとんど無限に貯蔵」できるわけがない。
③：デジタルデータは２進法の数字を演算することで、
情報伝達（ネット通信など）ができるし、データを記録して保存している。

問４
ある電力会社の１か月ごとの電気料金の仕組みは、１か月に消費した電力量に対して、次のような決まりになっているとする。ただし、消費税は考えずに計算する。

決まり１）20ｋＷｈまでの電力に対しては、すべての契約者が380円を支払う。
決まり２）20ｋＷｈを超えて120ｋＷｈまでの電力に対しては、1ｋＷｈあたり23円を加算する。
決まり３）120ｋＷｈを超えて300ｋＷｈまでの電力に対しては、1ｋＷｈあたり29円を加算する。
決まり４）300ｋＷｈを超えた電力に対しては、1ｋＷｈあたり33円を加算する。

例えば、１か月あたり100ｋＷｈの電力を消費した場合は、
380＋（100－20）×23の計算から、2220円の電気料金を支払うことになる。
１か月に280ｋＷｈの電力を消費したときの電気料金を求めよ。
7320円
*段階的に上がっていく料金体系の計算。
１段ごとに計算し、最後に合算。
380＋（120－20）×23＋（280－120）×29
＝380＋2300＋4640＝7320

問５
‹説明文›電気エネルギーが光エネルギーと熱エネルギーにそれぞれ変換されたときなどのように、
さまざまなエネルギーが、たがいに変換されても、エネルギーの総量は増えも減りもせず、
もとのままであることを「エネルギー（　　）の法則」という。
①変換　　②保存　　③加算　　④分割
②
*理科用語。

問６
電気エネルギーを得る方法〔発電〕にはさまざまな方法がある。
このことを説明している次の〔説明文〕のア～エに入る語の組み合わせとして
最も適するものを選びなさい。ただし、イは〔説明文〕の中２か所ある。
〔説明文〕
火力発電では、石油や天然ガスなどの燃料を燃やして高圧の水蒸気を発生させ、その力で発電機を回して発電する。燃料のもつ化学エネルギーを（　ア　）エネルギー、（　イ　）エネルギー、
電気エネルギー、の順に変換しているといえる。
水力発電では、ダムにたくわえた水で発電機につながる水車を回して発電する。ダムにたくわえられた水の（　ウ　）エネルギーを、発電機を回す（　イ　）エネルギーに変換して電気エネルギーを得ているといえる。
これらに対し、太陽光発電（太陽電池）は、太陽からの（　エ　）エネルギーを、半導体の性質を利用して、直接、電気エネルギーに変換していている。
①ア：熱　　イ：運動　ウ：位置　エ：光
②ア：熱　　イ：位置　ウ：運動　エ：光
③ア：運動　イ：光　　ウ：位置　エ：熱
④ア：位置　イ：光　　ウ：運動　エ：熱
①
*発電の過程で行われるエネルギーの変換を問う設問。
火力では、化学エネルギーを燃焼させて熱エネルギーへ。
熱は水を水蒸気として上にあげる。物体（水）を動かすので運動エネルギー。
水蒸気の運動でタービンを回すことで発電が行われる。
水力は、降水で高い場所にある水がもつ位置エネルギーを利用し、
水が落下する運動エネルギーでタービンを回して発電する。
太陽光はその名の通り、光エネルギーをもとに発電する。

問７
〔資料２〕の無いように基づいて書かれた下の‹英文›のア～エには、
それぞれＡ、Ｂのいずれかが入る。
Ａ：incandescent lamps（白熱電球）
Ｂ：LED lamps（ＬＥＤ電球）
ア～エに入る語を順番に示したものとして最も適するものを選びなさい。
ただし、文頭で大文字とすべき文字も小文字で表すこととする。
‹英文›
（　ア　）became popular in the early 20th century because it was easy to use them.
But now （　イ　） have become more popular than（　ウ　） 
because the energy efficiency（エネルギー変換効率） of（　エ　）is better.
①Ａ・Ｂ・Ｂ・Ａ　②Ｂ・Ａ・Ａ・Ｂ　③Ａ・Ｂ・Ａ・Ｂ　④Ｂ・Ａ・Ｂ・Ａ
③
*英文問題。空欄には白熱かＬＥＤがはいる。
直訳：『（　ア　）は20世紀初頭には人気であった。なぜなら、使いやすかったから。
しかし、今は（　イ　）が（　ウ　）よりも人気になっている。
なぜなら、（　エ　）のエネルギー変換効率よりも良いからだ』
内容はわかりやすいかと。

問８
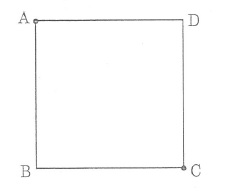
下の図のような、１辺の長さが２ｍの正方形ＡＢＣＤの点Ａにある光源から、
この正方形の内部に向けて出発した光線を考える。
この光線は、正方形の各辺で、入射角と反射角が等しくなるように反射し、
頂点に達するとそこで止まるものとする。また、正方形の内部では、光線は直進するものとする。
この光線が、正方形の辺で２回反射して点Ｃに到達したとき、光線が進んだ距離を求めよ。
ただし、答えに無理数がふくまれるときは、無理数のままにしておきなさい。
根号がふくまれるときは根号の中は最も小さい自然数にしなさい。
分母に根号がふくまれるときは、分母に根号をふくまない形にしなさい。
また、答えが分数になるとき、約分できる場合は約分しなさい。

２√10ｍ
*ラストに反射問題。
２回反射してＣにゴールするような経路を考える。

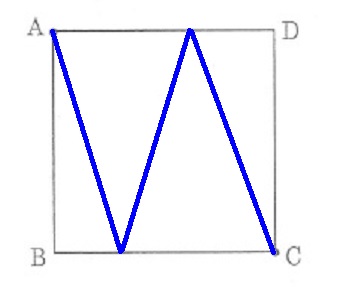
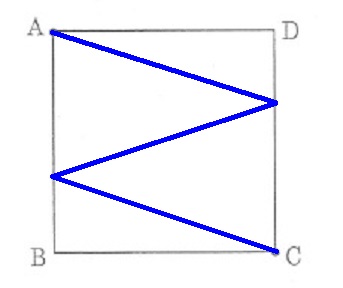
Ａから出発して上下か左右。ともに合計の距離は同じ。

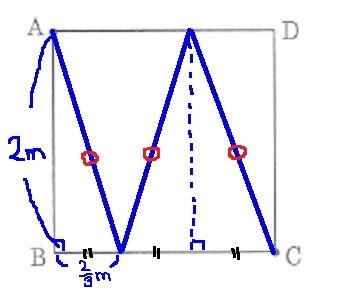
３つの合同な直角三角形があらわれる。
正方形の１辺を３等分するので、２/３ｍ。
三平方の定理から、
√{（２）²+（２/３）²}
＝√（４＋４/９）
＝√４０/９＝２√１０/３
これが３本なので、
2√１０/３×３＝２√１０ｍ

＠別解＠
反射の問題は鏡の世界をつくる。

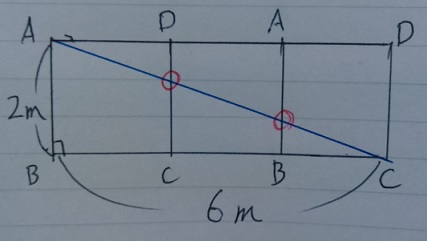
左のＡから出発してＣＤにぶつかったとき、
ＣＤを対象の軸として新しい正方形を右側にくっつけます。
同様に、新しいＡＢを対象の軸として正方形を対称移動。
３つの正方形で左上のＡから右下のＣにむけて１本の直線をひきます。
この青い線の長さが光線の移動距離。
赤い〇が反射するポイント。２か所あるので２回反射します。
三平方の定理から、√（２²＋６²）＝２√１０ｍ
難問特色検査の解説ページに戻る