2016年度　湘南高校・特色検査【大問３】問題解説

〔航海に必要な緯度経度から地球の全周を測定する〕
◆（ア）
本文中に「1872年の日本」「紀元前３世紀のエジプト」「1791年のフランス」「1773年のイギリス」についての記述がある。その頃のそれぞれの国家の状況について述べた次の文のうち、時期的に見て、明らかに誤っているものを選びなさい。
１：1872年頃の日本では、政府の殖産興業の政策のもと、岩倉具視を団長とする使節団が欧米諸国などに派遣され、官営模範工場として富岡製糸場が設立されていた。
２：紀元前３世紀頃のエジプトでは、ムハンマド（マホメット）によってアラビア半島で始められたイスラム教が伝わり、絶対神アラーへの信仰が盛んになった。
３：1791年頃のフランスでは、国王や貴族に対する民衆の不満からフランス革命が起こり、自由・平等や私有財産の尊重を掲げた人権宣言が発表された。
４：1773年頃のイギリスでは、産業革命が起こり、絹織物や紡績の機械が発明され、蒸気機関の改良などにより、生産力が飛躍的に増大しつつあった。
２
*２：エジプト王朝は前３世紀頃から始まったとされる。
エジプト国王を太陽神ラーの化身を意味するファラオとして崇めたという。
イスラム教の始まりは７世紀。公立高校入試でもテッパンの知識。
他の選択肢も一応確認しておこう。蒸気機関の改良はワット。

◆（イ）
本文中の（　あ　）～（　う　）にはてはまる、適切な数値を答えなさい。
～本文抜粋～
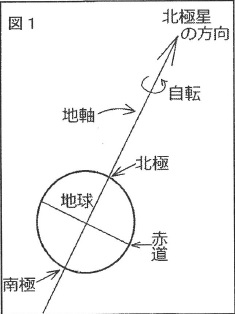
緯度は北極星の高度（水平線からの角度）を用いて比較的単純な原理から求めることができる。図１のように、北極星は地軸、つまり地球の自転の回転軸のほぼ延長線上にあり、北半球では季節や時刻にかかわらず北極のほぼ真上に見えているので、北極星の高度を測れば、その場所の緯度がわかるのである。地球が完全な球体で、北極星が地軸上にあると仮定し、大気中の光の屈折などの影響を無視できるとすると、北極星が真上に見える地点の北緯は（　あ　）度、北極星が水平線上に見える地点の北緯は（　い　）度、北極星の高度が30度になる地点の北緯は（　う　）度であると考えればよい。南半球では「天の南極」に相当する、天空上の天を用いて同様に南緯を求めることができる。
実際の測定ではその地点の標高や大気中の光の屈折などの誤差を考慮しなければならず、複雑な計算になるが、緯度は地球上のどこにいても、星が見えれば比較的単純な原理から求めることができ、そのときの時刻によって計算結果が変わることはない。

あ：90、い：０、う：30
*ここも正答率は高い。
北極星の高度＝その地点の緯度。北極星の高度を並べて終了。

◆（ウ）
下線部（Ａ）に関する、次の文中の（　Ⅰ　）に適切な数値を、（　Ⅱ　）に「増やす」または「減らす」の語のいずれかを入れなさい。
～本文抜粋～
一方、地球が太陽の周りを１回公転するのに要する時間を１年とした。それを１日の時間で割ると約365日となるのだが、実際には365.242190402・・日というように端数が出る。そのため、当初は１年を365日と決めていたが、４年で約１日分足りなくなり、長い間に季節がずれてしまった。そこで、_（Ａ）１年を365.25日の長さと考えて、４年に１度閏（うるう）年をおき、端数を調整することになった。それがユリウス暦である。しかし、それでもまだ季節とのずれが生じてきたため、16世紀後半になって、400年の間に３回閏年を減らすようにした。それが現行のグレゴリウス暦である。ちなみに、日本でグレゴリウス暦が採用されたのは1872（明治５）年であった。

『下線部（Ａ）のような調整を行っても、まだ公転周期とは正確に一致しないため、長い間には少しずつ季節とのずれが拡大していくことになる。仮に１年を365.2422日の長さと考えて暦を作るとすると、グレゴリウス暦の「４年に１度閏年をおき、400年の間に３回閏年を減らす」という方法に加えて、「10000年の間に（　Ⅰ　）回、閏年を（　Ⅱ　）」ことになる』
Ⅰ：３　Ⅱ：減らす
*差がつく問題。
実際の１年の長さは、365.242190402…日と小数が不規則につづくが、
ユリウス暦では365.25日と小数第３位以下を無視して切り上げたので、
実際の１年よりも多くの日数をカウントすることになる。
年数を経るたびにズレが大きくなったので、グレゴリオ暦では400年に３回、閏年を減らした。

今、グレゴリオ暦のもととなる〔１年＝365.25日〕から〔１年＝365.2422日〕に変えると、
実際の公転周期の値である365.242190402・・日に近づくが、それでもこれより値が大きい。
ということは、実際の公転周期よりも多くの日数をカウントしているので、
正確性を期するために閏年を減らさなければならない。（Ⅱは”減らす”になる）

減らす回数の計算は、１年あたりの平均日数をベースに考えるのがポイント！
１年は365日。４年に１度は閏年なので、１年あたりの平均日数は【365＋１/４日】。
400年に３回、閏年を減らすので、１年あたりの平均日数は【365＋１/４－３/400日】。
この計算結果と、１年の日数として設定した365.2422日との差が１年で生じるズレとなり、
それを１万倍すれば１万年間の差となる。
（365＋１/４－３/400－365.2422）×１万
＝（365＋0.25－0.0075－365.2422）×１万
＝0.0003×１万＝３日

１万年で３日分のズレが多く生ずるので、１万年に３回閏年を減らせばよいことになる。

◆（エ）
下線部（Ｂ）について、「ある角度」（後述）とはどの角度か。
図３の点Ｎ、Ｏ、Ｐ、Ｑ、Ｒを用いて、「∠ＡＢＣ」のように答えなさい。

～本文抜粋～
図３と図４を見てみよう。エジプトのナイル川沿岸の都市シエネでは毎年夏至の日の南中時刻になると太陽が真上に来るため影ができない、ということが知られていた。紀元前３世紀、エジプトで活躍した天文学者エラトステネスが、このことに着目して、地球の大きさ（全周）を計算して求めた。シエネはほぼ北回帰線上に位置していた。一方、その北に位置するナイル川河口付近のアレクサンドリアでは、同日南中時刻に太陽は真上より少し南に傾いた位置にあり、太陽の高度は82.8度であった。水平な地面に垂直に立てた棒には、地面から82.8度の角度で影ができるのである。
エラトステネスはナイル川はほぼ南北に流れており、２つの都市は同一子午線上にあると考えた（実際には東西に約300ｋｍずれている）。彼は地球を完全な球体と仮定し、_（Ｂ）アレクサンドリアとシエネにおける太陽の高度の差が、地球の全周を求めるために役立つある角度と同じであると考え、シエネとアレクサンドリアの距離から地球の全周を約１割の誤差で計算することができた。

∠ＰＯＱ
*地球全周を求めるのに役立つ角度から、なんとなく察せてしまう。

太陽は地球から遠くにある天体なので、
シエネとアレクサンドリアに注ぐ太陽光は平行とみなせる。
同位角でおろすと∠ＰＯＱとなる。
∠ＰＯＱはアレクサンドリアとシエネの緯度の差にあたる。
アレクサンドリアとシエネを同一子午線上にあるとしたうえで、
２地点の距離×360°/緯度の差＝地球の全周となる。

◆（オ）
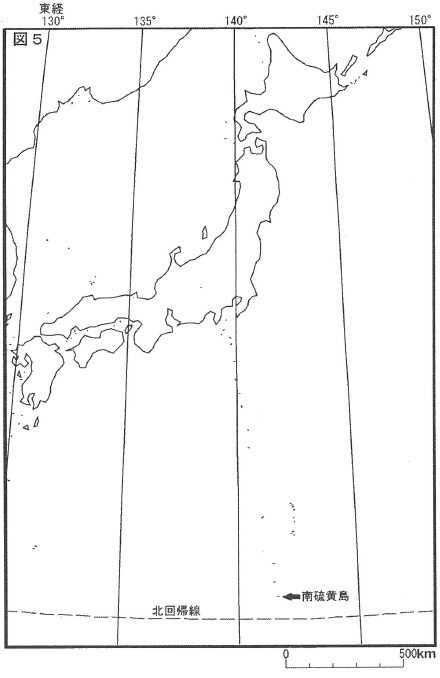
図５は日本周辺の略地図である。地図を見て、次の問いに答えなさい。
（ｉ）
南硫黄島は北回帰線（夏至の日に太陽が真上にくる緯線）の近くに位置している。夏至の日の、南硫黄島における南中時刻は、日本標準時の基準となっている明石における南中時刻に対して、どれくらいずれているか、次のなかから正しいものを選びなさい。

１：約25分前　２：約15分前　３：約５分前
４：約５分後　５：約15分後　６：約25分後
１
*基本レベルゆえ必答。
日本の標準時は東経135度。
南硫黄島はこれより東になるので、明石より早く南中する⇒１～３
経度15度で１時間ズレるので、５度の差で20分のズレが生じる。
東経135度線から南硫黄島は５度以上、経度の差があるので１。

（ii）
夏至の日の湘南高校での南中時刻における太陽の高度について、次の文中の（　Ⅰ　）と（　Ⅱ　）にあてはまるものを１つずつ選びなさい。なお、地図中における藤沢市と任意の１地点との距離は正しく表されているものとする（地球の全周は40000ｋｍとする）。

「藤沢市と北回帰線との距離は、地図からおよそ（　Ⅰ　）ｋｍとわかるので、湘南高校における太陽の高度はおよそ（　Ⅱ　）度となる」
ａ：700　ｂ：1000　ｃ：1300　ｄ：1600　ｅ：1900　ｆ：2200
ｇ：12　ｈ：23　ｉ：34　ｊ：45　ｋ：56　ｌ：67　ｍ：78
Ⅰ：ｃ　Ⅱ：ｍ
*Ⅰ：地図下の縮尺から、500ｋｍの２倍強なのでｃ（1300ｋｍ）。
Ⅱ：２問前の考えを用いる。
【２地点の距離×360°/２地点の緯度の差＝地球の全周】
360°　…　40000ｋｍ（全周）
？° 　…　1300ｋｍ（湘南～南硫黄島）
？＝360×1300/40000＝11.7°

南中高度は、90－11.7＝78.3°
11.7°ではないことに注意！夏の湘南で南中高度が10°はありえない。

◆（カ）
下線部（Ｃ）に関連して、日本における１ｍの長さの基準になった「日本メートル原器」は白金とイリジウムという金属の合金でできている。初め、メートル原器は、２点間の０℃における距離（地球全周の4000万分の１の長さ）で１ｍを定義していたが、のちに目盛線の引き直しがおこなわれた（現在では１ｍは光を使って定義されている）。
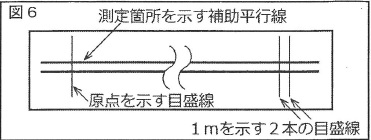
図６は目盛線が引き直されたあとのメートル原器を示した概念図である。左端に原点を示す目盛線があり、右端に１ｍを示す目盛線が２本引かれている。２本のうち、１本は０℃、もう１本は20℃における目盛線である、２本のうち、20℃における目盛線はどちらか。「右」、「左」のいずれかで答え、その根拠を示す次の文中の（　　）にあてはまるように、15字以内で答えなさい。

「金属製のメートル原器は、（　　　）から」
左、根拠－温度が高くなると膨張する
*根拠から考える。温度が高くなると金属は膨張する。
膨張するとメートル原器が示す１ｍも膨張で長くなってしまう。
だから、短い目盛り線（左）が20℃における正しい１ｍを指す。

◆（キ）
下線部（Ｄ）に関連して、不正確な時計を使用して航海した場合、経度や位置の計算にどれだけの誤差が生じるだろうか。北緯60度・経度０度の場所に停泊している船の上で太陽の観測を行い、正確な時計を使って経度の計算を行った結果、もし仮にちょうど10分進んでいる時計を使用して同じように計算したとすると、計算による位置は、経度何度にいるという結果になってしまうか。また、このときの計算による位置は、実際にいる位置から、北緯60度線上で何ｋｍずれてしまうか。次の文中の（　Ⅰ　）に「東」または「西」を、（　Ⅱ　）と（　Ⅲ　）に適切な数値を入れなさい。ただし、地球が完全な球体で、その全周が40000ｋｍであるとする。また、答えに端数が出る場合は、小数第２位を四捨五入し、小数第１位まで答えること。

「（　Ⅰ　）経（　Ⅱ　）度にいるという結果になり、
北緯60度線上で（　Ⅲ　）ｋｍずれてしまう」
Ⅰ：西　Ⅱ：2.5　Ⅲ：138.9
*最後の設問でやや難だが、湘南高校を目指す生徒であれば解けるようにしたい。
船は【北緯60度、経度０度】にいる。
この地点の南中時刻が仮に12：00であった場合、
10分進んだ時計で計測すると12：10に南中したことになる。
つまり、南中時刻が10分遅れて計測されるので、実際の場所より西側にあるという結果になる。

経度が15度ズレると60分の差が生まれるので、
15度×10/60＝2.5度⇒船は【西経2.5度】にいることになる。

北緯60度線上のズレは、地球の断面を描いて60°を活用する。

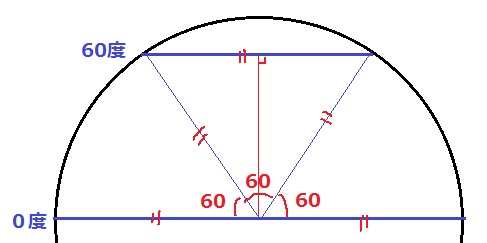
条件から地球は完全な球体を考えるので、半径を作図すると正三角形が現れる。

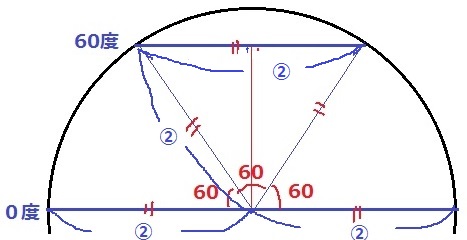
北緯60度線の直径を②とおくと、０度の直径は④。
赤道の円周の半分が北緯60度線の円周にあたる。
その円周の2.5度分の弧の長さが答え。
40000ｋｍ÷２×2.5/360＝1250/９＝138.888…⇒138.9ｋｍ

60度線の10分の違いで140ｋｍほどズレが生じるので、
北緯35度線上ではもっとズレますね((( ;ﾟдﾟ))

～本文要約～
緯度の測定は北極星の観測から導けるが、経度の測定は困難を極めた。太陽は１時間に経度にして15°度分動くが、太陽の位置とその地点の経度とそのときの時刻は互いに連動しているので、周囲に目印となるものがない海上で、無線通信や人工衛星がなかった時代では、経度の測定に正確な時計が必要であった。そこで、イギリス政府は高い報奨金を出して、船舶の正確な位置を測定するための方法を開発させようとした。
その報奨金を獲得したのは大工職人のジョン・ハリソンであった。彼は1759年に「クロノメーター（航海用の高精度の時計）Ｈ４」を完成させた。当時、精巧な時計でも10日で約10分の誤差が生じるのが普通だったのに対し、彼の時計は約２ヶ月の航海でわずか約５秒の誤差にとどまったといわれる。この発明により、航海の際に海図上の船の位置を調べる技術が格段に進歩した。

時の話より。現在の日本円に直すと３億９千万ほどの報奨金を得たという。
歴史を動かした時計ですから安い方かもしれませんね？
難問特色検査の解説ページに戻る