◆（ア）
〔衣服の取扱い表示に関するリード文〕
（ａ）
私たちの身の回りの商品には、衣類の取扱い表示以外にも、さまざまなマークがついている。
型式、形状、寸法や品質などが、経済産業省などの機関が定めた規格に適合していることを
示すマークとして正しいものを選びなさい。
３
*経済産業省絡みのマークを選ぶ。答えは有名なマークなので当てておきたい。
正解は３のＪＩＳ（ジス）マークとよばれる、工業品につけられるマーク。
経産省にある日本工業標準調査会が審査する。
１：ＪＡＳマーク。農作物などにつけられるマークで農林水産省の管轄。
２：ＳＧマーク。スポーツ用品や台所用品、福祉用品など幅広い品目の安全性を保証する。
４：Ｇマーク。グッドデザイン賞を受賞したものにつけられる。
５：Ｒマーク（再生紙使用マーク）。古紙パルプ配合率を示す。数字は配合率。Ｒ80だったら80％。
（ｂ）
下線部Ａ『組成表示（毛50％ポリエステル50％）』とあるが、
学生服は混紡（こんぼう；質の異なる繊維を混合して作られたもの）が多い。
これはそれぞれの繊維の長所を生かして、短所を補い合うためである。
学生服の生地として使われる場合に、一般的に「毛100％」および「ポリエステル100％」の短所とされることを、次の中からそれぞれ１つずつ選びなさい。
１：ぬれると弱くなる。 ２：水で洗うと伸びやすい。 ３：湿気を吸わない。
４：しわになりやすい。 ５：虫の害を受けやすい。
毛―５ ポリエステル―３
*公立だから実技教科も大切にということでしょうか。
天然繊維である毛は湿気を吸い、保湿や保温に優れているが、
反面、虫に食われやすく、水で洗うと縮む。
合成繊維であるポリエステルは耐久性があり、シワになりにくいが、
湿気をあまり吸わず、静電気が発生しやすい。
（ｃ）
下線部Ｂ『取扱い表示』とあるが、湘太くんが昨年３月に買った学生服には、
図のような取扱い表示がついていた。これをふまえ、適切ではないことを２つ選びなさい。
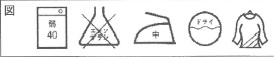←左２つは『弱40』『エンソサラシ』と書かれてある。
１：塩素系漂白剤で漂白する。 ２：クリーニング店に出す。
３：150度の温度でアイロンをかける。 ４：手洗いする。
５：弱水流コースで洗濯機にかける。 ６：日当たりのよい場所に干す。
１・６
*家庭科ニガテだったな(;´д｀)
旧表示。左から順に、
〔洗濯の際の液温は４０℃が限度、洗濯機で弱洗いができる〕
〔塩素系漂白剤の使用禁止〕
〔中温度でのアイロンがけＯＫ〕
低温度・・80-120℃ 中温度・・140-160度 高温度・・180-210℃
〔ドライクリーニングＯＫ〕
ドライクリーニング・・水を使わず、有機溶剤で洗う。クリーニング店でやってくれる。
〔日陰でつり干し〕
（ｄ）
下線部Ｃ『日本では、約半世紀にわたって独自の取扱い表示が使われてきたが、
昨年12月1日に全面的に変更された』とあるが、なぜ日本の取扱い表示は変更されたのだろうか。
その考えられる理由として、明らかに誤っているものを選びなさい。
１：日本で生産された衣類を、日本で購入する外国人が増えたため。
２：国際規格でも、洗濯物を屋外に干すことが多い日本の習慣に対応できるようになったため。
３：海外でナイロンなどの新しい繊維が開発されたことにより、洗濯の仕方が多様化したため。
４：輸出入の際に商品につける取扱い表示を差し替える手間を省けるようにするため。
３
*日本独自の取扱い表示が国内外で統一された理由を問う。
１：日本の服を買った外国人にとって表示の統一化はありがたい。○
２：国際規格でも日本の習慣に対応できるようになれば、
統一化による表示の変更があっても日本人にとって弊害も少ない。○
３：洗濯の仕方が増えたことで、表示の種類が増えるかもしれないが統一化には結びつかない。×
４：統一化により、日本の表示と外国の表示を差し替える作業がなくなる。
ちなみに、ナイロンは1935年、アメリカで発明された世界初の合成繊維らしい。
◆（イ）
次の文章を読んで、１～５の説明に合うように、あとの（ａ）の文中の空欄に入る英語と、
（ｂ）の文中の空欄に入る数字を答えなさい。
（ａ）Where does Emma live? ― She lives on the 〔 〕 floor.
（b）What is the room number of Fiora’s room? ― It is 〔 〕.
ａ：second b：33
*英文推論問題。
英文自体はやさしい。前半は、図の家の解説なのでササッと読んでしまうこと。
～和訳～
３階立ての大きな家がある。１階には２つの部屋と台所があり、２階には３つの部屋、３階にも３つの部屋があり、この家には８つの部屋があります。各部屋には番号がつけられています。11・12・21・22・23・31・32・33。11・12の部屋は１階、21・22・23の部屋は２階、31・32・33の部屋は３階にあります。11・21・31の部屋の隣には階段があります。
エイミー、ベティ、カーラ、デイジー、エマ、フィオラ、ジーナの７名がこの家に住んでいます。
１人につき１つの部屋を持っており、１つの部屋は誰も使っていません。
１；ベティは２階に住んでおり、その階には２人しかいません。
２；エイミーの部屋はフィオラの隣ですが。フォオラの部屋の隣には誰もいません。
３；カーラとジーナは隣同士で、その階には２人しかいません。
４；デイジーの階には３人います。
５；デイジーの部屋の隣には階段があります。
１より、２階にはベティーと誰かと空き部屋。
４から、デイジーのいるフロアには３人いるが、１階と２階は２人しかないので３階。
５から、デイジーの部屋は３１。
３より、カーラ＆ジーナは２人しかいないフロアなので、２階にはベティがいるから11か12。
２より、エイミー＆フィオラの組み合わせは３階の32・33の組み合わせしかない。
そのうち、フィオラはエイミー以外と隣り合わないので、33がフィオラ、32がエイミーとなる。
情報のないエマは、２階にいることになる。
◆（ウ）
（ａ）
Ｔを図３で示した状態から滑らせずにウの位置に転がすと黒丸（●）が１個の面が底面になった。
その状態を上から見たとき、Ｔはどのように見えるか。底面以外の３つの面の黒丸（●）の配置を、解答欄の白丸（○）を塗りつぶすことによって示しなさい。
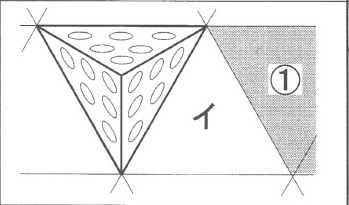
*図３から左のウにコロっと転がしたとき、上からみえる●の位置を求める。
サイコロ問題はよくみるが、今回は正四面体。
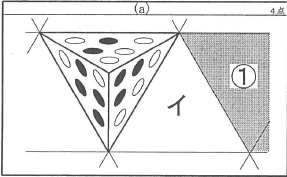←答え
●でイメージがわきにくかったら、○でイメージしてもＯＫ！
３個の面は図２に底面を書き込んでしまおう。
右下に３つ固まる。
これをウに移動すると○３つが最下段の横にきて、●３つが上にくる。
（ｂ）
Ｔを図３で示した状態から図１の①⇒②⇒③⇒④⇒⑤⇒⑥⇒⑦の順に滑らせずに転がしていったとき、
①～⑦の７つの位置におけるＴの底面に描かれていた黒丸（●）の個数の合計を求めなさい。
１７個
*①から⑦までコロがしたときに底面にある●の合計を数える。
●の位置は不要なので、数だけ調べる。
正三角形のマスを３つに分けて、側面にある●の数をひたすら書き込む。
イの状態は、１、２、４.
そこから右に移動して①にくると、１と４は見え、２が底面で消え、新たに３がでてくる。
コツは残る側面がわかりやすいので、ソチラを優先に書き込み、
手前のマスで表れなかった数字は後ろの側面にくること。
①は１、３、４が書き込まれているので底面は２。
②は４、③は１、④３、⑤４、⑥２、⑦１、全てたすと１７。
中学受験のやり方だが、これが一番ミスが少ないかと思われる。
◆（エ）
（ａ）
本文中の〔 あ 〕、〔 い 〕に入れるのに最も適するものを、それぞれ選びなさい。
１：する前 ２：したとき ３：した後 ４：時計回り ５：反時計回り
あ―１ い―４
*頭ぐちゃぐちゃになりそうな問題。
４０Ｈｚ（１秒間に４０回点滅）だと、円板がちょうど１回転したときに光がパシャっと当てられる。４１Ｈｚは１秒間に４１回、先ほどと比べて１秒の間に１回分おおく光が点滅するということは、光が照射される間隔が狭くなる。
つまり、40Ｈｚのペースで回転する円板が１周しないうちに次の光があてられるため、
○は円の上部より右側にくる（○は360度を回らないうちにストロボの光で姿を見せる）。
これが連続すると、右回り、すなわち、時計回りに回転しているように見える。
（ｂ）
図１の円板を回転数４０Ｈｚで回転させ、ストロボスコープの周波数に変えたとき、
円板上の白丸は何個あるように見えるか。次のページの表中の〔 う 〕〔 え 〕に入る数を答えなさい。
う―３ え―３
*少々強引だが、【Ｈｚを速さとして、この速さは距離と反比例】と考えるとわかりやすい。
速いと移動距離が短くなり、遅いと移動距離が長くなる（奇妙だが）。
理由は、Ｈｚが大きくなるとストロボからでる光の間隔が小さくなるので（チカチカの回数が増えるので）、
光っていないときの○の移動距離が短くなってしまうから。
４０Ｈｚで１秒１周。８０Ｈｚは２倍速で、１秒半周。
１２０Ｈｚは３倍速なので、１秒で３分の１。
３０Ｈｚ：４０Ｈｚ＝３：４ 移動距離は逆比で４：３。
４０Ｈｚで１周なので、３０Ｈｚでは、１周×４/３＝４/３周＝１・１/３周
１周と３分の１周。端数分の３分の１（１２０°）がズレとして○が移動してみえる。
つまり、円を３分の１して、１２０°間隔で○があらわれる。よって、３個。
６０Ｈｚも同様。４０Ｈｚ：６０Ｈｚ＝２：３
移動距離は逆比で３：２。
１周×２/３＝２/３周
６０Ｈｚの場合、２４０°のズレであらわれる。
結局は、円を３分の１に分けたうちのいずれかの場所にあらわれるので、３個となる。
＠１００Ｈｚで５個の理由＠
表中の１００Ｈｚを試してみる。
４０Ｈｚ：１００Ｈｚ＝２：５ 移動距離は逆比で５：２
１周×２/５＝２/５周
分母に５がでてくるということは、円を５つにわけたうちのいずれかにくる。
よって、５個。
（ｃ）
次の１～４のような図形が描かれている円板を、回転数４０Ｈｚでそれぞれ回転させ、
ストロボスコープの周波数を８０Ｈｚにして観察した。
そのとき、実際に描かれている図形と同じように見えるものをすべて選びなさい。
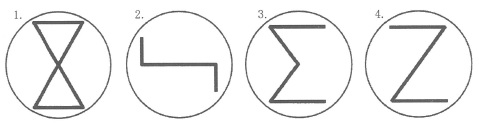
１、２、４
*４０Ｈｚから８０Ｈｚにしても同じく見える図形を選ぶ。
８０Ｈｚは半周。１８０°回転しても同じな図形、いわゆる点対象の図形を選べばおしまい。
（ｄ）
ある図形を描いた円板を回転数４０Ｈｚで回転させたとする。
ストロボスコープの周波数を１２０Ｈｚにして観察すると、図４のように見えた。
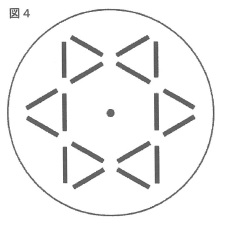
図４の１８本の線はすべて同じ長さである。
また、ストロボスコープの周波数を８０Ｈｚに変えて観察すると、
実際に描かれている図形と同じように見えた。
円板に描かれている図形として、使われている線の本数が最も少ないものを答えなさい。
なお、解答は解答欄の図中の細線を太く濃くなぞることによって示しなさい。
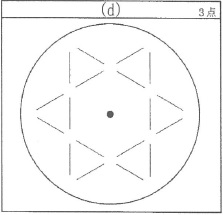
*解答例↓このいずれかであれば正解○
また、下の解答例を回転移動させたものもすべて正解◎
１２０Ｈｚは３分の１ずつズレる。
図４の図形は１８本の辺からなるので、１８÷３＝６本の辺を塗りつぶせばよい。
場所は、３分の１ずつズラして３回ですべての辺が塗りつぶされるところ。
上の解答例で、黒い辺を中心から120°ずつズラして塗りつぶしていくと、３回目で図４になる。
難問特色検査の解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント