2019年度　石川県公立高校過去問【数学】解説

平均49.6点

記述問題が多く、配点も大きいです。
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）ア
５－（－２）
＝５＋２＝７

イ
－２×（－３）²＋４
＝－18＋４＝－14

ウ
２ｘ³ｙ²÷１/２ｘｙ²
＝４ｘ²

エ
（ａ＋２ｂ）/３－（ａ－ｂ）/２
＝{２（ａ＋２ｂ）－３（ａ－ｂ）}/６
＝（－ａ＋７ｂ）/６

オ
√12－３√２÷√６
＝２√３－√３＝√３

（２）
２ｘ²－３ｘ－１＝０
解の公式を適用。
ｘ＝（３±√17）/４

（３）
積が５→少なくとも１つが５。
（大、小）＝（１、５）（２、５）（３、５）（４、５）（６、５）
これらの反対の組み合わせもＯＫ。
これに（５、５）を加え、計11通り。
全体は、６×６＝36通り
11/36

（４）
ｙの変域に負の数がでてくるので、傾きａは負。
ｘ＝２のとき、最小値ｙ＝－12（ｘ＝０のとき、最大値ｙ＝０）
ｘ＝２、ｙ＝－12をｙ＝ａｘ²に代入。
－12＝４ａ
ａ＝－３

（５）
10人の中央値は、５番目と６番目の平均値。

線分図で整理。差が４なので、中央値から２離れている。
５番目が23で、６番目が27。

11人の中央値は、（11＋１）÷２＝６番目の生徒の値。
Ａは28回なので、６番目は27回→中央値は27。

大問２（規則）

（１）
ＰとＱがＡにいるとき、正六角形の１周である６ｍ離れている。
動き始めると、１秒で３ｃｍずつあいだが縮まるので、
６÷３＝２秒後に出会う。

（２）
説明も記述する（図、表も用いてＯＫ）。
１秒後にＰとＱはＣで重なる。
前問より２秒間隔で重なるので、
重なる点を調べると【Ｃ→Ａ→Ｅ→Ｃ→Ａ→Ｅ…】とループする。
Ｃから２周して（12ｍ動いて）再びＣで重なる。
Ｐが動く長さは、２、２＋12×１、２＋12×2、２＋12×３…
Ｃでｎ回出会うとき、Ｐの動く長さは、２＋12（ｎ－１）＝12ｎ－10

大問３（数量変化）

（１）
基本料金…1000円
使用量ごとの料金…20円×４ｍ³＝80円
計1080円

（２）
（20、2200）と（30、3700）が通る式を求める。
変化の割合ａ＝（3700－2200）/（30－20）＝150
ｙ＝ａｘ＋ｂにａ＝150、ｘ＝20、ｙ＝2200を放り込む。
2200＝150×20＋ｂ
ｂ＝－800
ｙ＝150ｘ－800

（３）
条件にそった料金設定を考える。過程も記述する。
基本料金を700円にし、B市での水道料金と比較して、
20ｍ³～30ｍ³まではB市より高く、30ｍ³～はB市よりも安く設定する。
（20ｍ³未満は考えない！）

出発点は（０、700）。
これと（20、2200）を通る直線と（30、3700）を通る直線の内側にあればいい。
（０、700）→（20、2200）
（2200－700）/20＝75
（０、700）→（30、3700）
（3700－700）/30＝100
傾きが75より大きく100より小さい範囲にあればよい。
使用量ごとの料金でいえば、１ｍ³あたり75円より高く100円より安くすればいい。

大問４（方程式）

方程式の説明記述。
問題文では小麦粉と売り上げの話しかないので、それ以外の情報は見ない。
ドーナツをｘ個、カップケーキｙ個で連立を組む。
40ｘ＋30ｙ＝4000
100ｘ＋150ｙ＝15400
これを解いて、ｘ＝46、ｙ＝72
ドーナツ…46個、カップケーキ…72個
*配点が10点で、立式ができれば答えもでやすいので取りこぼしたくない。

大問５（作図）

①ＡＰ＝ＣＰ
⇒ＡＣの垂直二等分線上にＰがある。

②直径ＢＰの円周上にＣがある
→円周角の定理から、半円の弧に対する円周角は直角→∠ＢＣＰ＝90°
⇒Ｃを通りＢＣに垂直な直線をひく。

２本の直線の交点が点Ｐとなる。
*配点は８点。ＢＰを直径とした円の円周にＣを描いてみると、②は思いつきやすい。

大問６（平面図形）

（１）

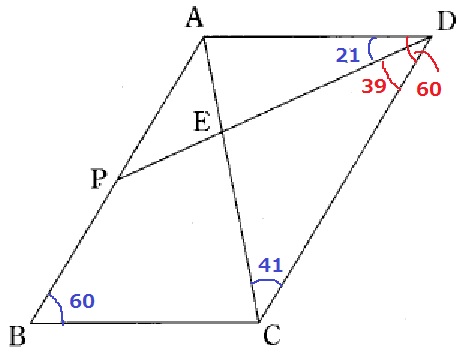
平行四辺形の対角は等しい。
∠ＡＤＣ＝60°
∠ＥＤＣ＝60－21＝39°
△ＣＤＥの内角で、∠ＣＥＤ＝180－（39＋41）＝100°

（２）
△ＧＣＤ∽△ＱＰＦの証明。

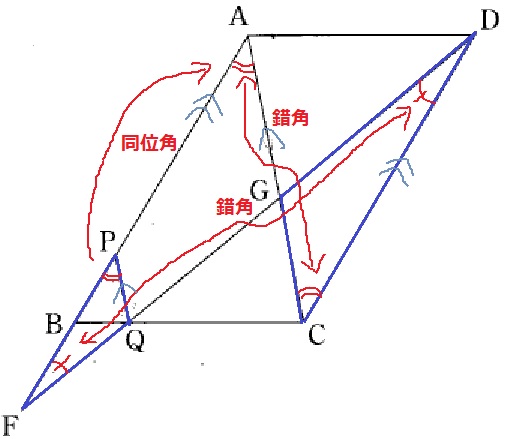
辺の情報が乏しいので、角度を操作する。
２組の平行線から同位角と錯角を利用して２角が等しい→∽
∠ＦＱＰ＝∠ＱＧＡ＝∠ＤＧＣ（同位角⇒対頂角）でもＯＫ！

（３）
ここも途中式を解答する。
まずは作図。
ＣＰ＋ＰＤが最短→反射の問題は対称移動させて直線。
ＡＢを対称の軸として、Ｃの移動先をＣ’とおく。

↑正確な図ではありません。。
Ｃ’ＤがＣＰ＋ＰＤの最短距離にあたる（Ｃ’ＤとＡＢとの交点がＰ）。
∠ＡＢＣ＝60°を活用する。
対応する点ＣとＣ’を結んだ線分と対称の軸ＡＢは垂直に交わる。
30°－60°－90°の直角三角形を発見。
１：２：√３から、４×√３/２＝２√３
ＣＣ’＝２√３×２＝４√３

平行四辺形の内角である∠ＢＣＤは、180－60（∠ＡＢＣ）＝120°
∠Ｃ’ＣＤ＝120－30＝90°
△Ｃ’ＣＤで三平方。
Ｃ’Ｄ＝√（４√３²＋６²）＝√84＝２√21ｃｍ

大問７（空間図形）

（１）
ＡＢ以外の横線が答え。
辺ＤＣ、辺ＥＦ、辺ＨＧ。

（２）
四角形ＣＰＥＱの各辺を斜辺とする、外側にある４つの直角三角形に刮目。

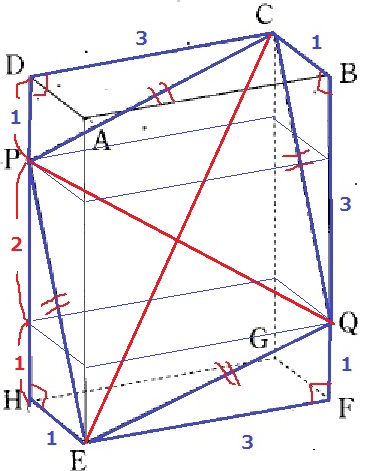
どれも３ｃｍと１ｃｍで、２辺とあいだの角が同じ。
△ＰＣＤ≡△ＥＰＨ≡△ＱＥＦ≡△ＣＱＢ
ということは、四角形ＣＰＥＱは菱形。
菱形の面積は、対角線×対角線÷２。

直方体（各辺の長さａ、ｂ、ｃ）の対角線の長さ⇒√（ａ²＋ｂ²＋ｃ²）
ＣＥ＝√（３²＋１²＋4²）＝√26ｃｍ

ＰＱを対角線とする直方体の高さは、４－１－１＝２ｃｍ
ＰＱ＝√（３²＋１²＋２²）＝√14ｃｍ

したがって、√26×√14÷２　←２を√４にすると根号付きで約分可
＝√26×√14÷√４＝√91ｃｍ

（３）
途中式の書き込みあり。

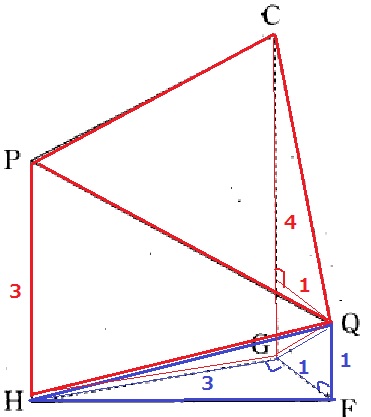
上のように、四角錘と三角錐に分ける。
（３＋４）×３÷２×１÷３＋３×１÷２×１÷３
＝４ｃｍ³

＠別解＠
柱体の斜め切断は、【底面積×高さの平均】で体積が求められる。

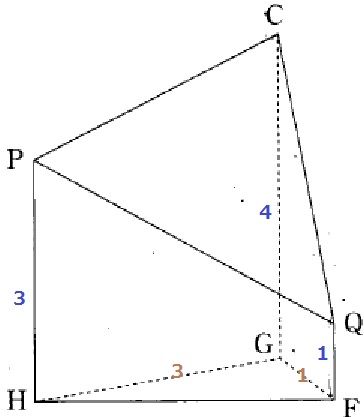
高さの平均…（３＋４＋１）÷３＝８/３
底面積は、３×１÷２＝３/２
３/２×８/３＝４ｃｍ³
公立高校入試解説ページに戻る