2020年度　栄光学園中学過去問【理科】解説

問題ＰＤＦ
必要ならば以下の値を使ってもよい。

【１】
次に示した植物Ａ～Ｄの名前を１つずつ選びなさい。
図の縮尺は同じとは限りません。

ア：イネ　イ：ススキ　ウ：コムギ　エ：エノコログサ

【２】
小麦粉にはデンプンが多くふくまれていますが、他の成分もふくまれています。
スパゲッティの材料となる小麦粉に水を加えてねり混ぜるとグルテンができます。
水の中でもみ洗いすると、デンプンが外に流されてグルテンを取り出せます。
グルテンはスパゲッティの「こし」の強さのもとになります。
問１
デンプンは、おもにエネルギーのもとになる栄養素です。
この栄養素の種類として、最も適当なものを選びなさい。
ア：炭水化物　イ：脂質　ウ：たんぱく質　エ：ビタミン

問２
グルテンについて説明した次の文の空欄①に入る栄養素の種類として、
最も適当なものを選びなさい。
「グルテンは、〔　①　〕の一種です。〔　①　〕はおもに体をつくるもとになる栄養素です。」
ア：炭水化物　イ：脂質　ウ：たんぱく質　エ：ビタミン

【３】
栄一君は乾燥したスパゲッティの強さに興味を持ち、スパゲッティの太さと長さと、
強さの関係を調べることにしました。

ふつうのスパゲッティは細長い円柱形をしています。まず、直径1.68ｍｍのスパゲッティを100本とり、まとめて重さをはかりました。結果は82.5ｇでした。次に、この100本から１本ずつとって長さを測りました。結果は表１のようになりました。

問１
直径1.68ｍｍのスパゲッティの平均の長さは何ｍｍですか。小数第１位まで求めなさい。

スパゲッティをわずかに曲げて両端をおさえるように持ち、少しずつ力をかけて曲げていくと、はじめのうちはしなり（力を受けて曲がること）が大きくなりますが、ある強さの力になるとスパゲッティは急にくだけて数本のかけらになります。このときの力の強さとスパゲッティの太さや長さの関係を調べてみることにしました。直径1.28ｍｍ、1.45ｍｍ、1.68ｍｍ、1.85ｍｍの４種類のスパゲッティを用意しました。各直径のスパゲッティを100ｍｍ、120ｍｍ、140ｍｍ、160ｍｍ、180ｍｍの長さに10本ずつ切断しました。１本ずつについて以下の操作をしました。

１：キッチンスケール（はかり）の上に軽いゴム板とスパゲッティ１本をのせ、
このときに表示の値が０になるように調整した。

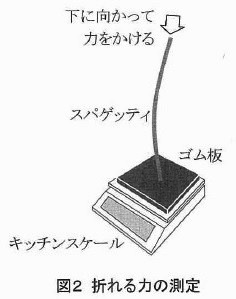
２：ゴム板の上にスパゲッティを垂直に立て、スパゲッティの上の端を手でおさえた。
３：はじめスパゲッティを少しだけ横向きにしならせてから、折れるまで、
　下に向かって力を少しずつかけていった。
４：スパゲッティが折れる直前にキッチンスケールで表示されていた重さの値（単位ｇ）を、
　スパゲッティが折れる力として記録した。

太さと長さが同じスパゲッティ10本の折れる力の平均値をそれぞれ求めました。
結果は表２のようになりました。

問２
直径1.68ｍｍのスパゲッティと直径1.85ｍｍのスパゲッティは、成分も長さの平均値も同じであるとします。直径1.85ｍｍのスパゲッティ１本の重さは、直径1.68ｍｍのスパゲッティ１本の重さの何倍ですか。小数第１位まで求めなさい。

問３
横軸をスパゲッティの長さ、縦軸をスパゲッティの折れる力として、４種類のスパゲッティの測定の結果をグラフに表しなさい。直径のちがいが分かるように示しなさい。

問４
横軸をスパゲッティの直径、縦軸をスパゲッティが折れる力として、長さ100ｍｍ、140ｍｍ、180ｍｍのスパゲッティの測定の結果をグラフで表しなさい。長さのちがいが分かるように示しなさい。

栄一くんは、ブカティーニという、スパゲッティに似たものがお店で売られているのを見つけ、
買って家に帰りました。

ブカティーニは全体としてストローのような形をしており、断面の中心には図４のように円形の穴があいています。１本あたりの平均値は、長さが257.6ｍｍ、重さが2.07ｇでした。またブカティーニの外径は2.78ｍｍでした。ブカティーニの成分はスパゲッティと同じであるとみなします。
今までの結果から、ブカティーニの重さは、同じ長さで直径1.68ｍｍのスパゲッティの約2.4倍だと計算できます。

問５
次の式は、同じ長さで比べた場合に、ブカティーニの重さが直径1.68ｍｍのスパゲッティの何倍かを求めるものです。空欄Ａ～Ｄにあてはまる数をそれぞれ、今までの問題文中の数値や解答欄の数値から選んで答えなさい。
〔　Ａ　〕÷〔　Ｂ　〕×〔　Ｃ　〕÷（〔　Ｄ　〕÷100）

スパゲッティと同じ方法でブカティーニが折れる力をはかり、ブカティーニの長さと折れる力の関係をグラフにしたところ、表３および図５のようになりました。

栄一君はこれらの実験結果から、スパゲッティやブカティーニの折れる力について次のように考えました。

〔１〕スパゲッティの折れる力は、同じ長さで比べたとき　　　①　　　、
同じ太さで比べたときは　　　②　　　ことがわかった。
〔２〕スパゲッティの太さと折れる力の強さの間には決まった関係がありそうだ。学校の先生のアドバイスから、すでにかいた長さ140ｍｍのスパゲッティの「直径と折れる力の関係」のグラフ（問４の答）の他に、
「直径に直径をかけた値と折れる力の関係」（図６）
「直径に直径を２回かけた値と折れる力の関係」（図７）
「直径に直径を３回かけた値と折れる力の関係」（図８）
「直径に直径を４回かけた値と折れる力の関係」（図９）のグラフをそれぞれかいてみた。

これらのグラフをくらべて見た結果、どの直径のスパゲッティでも「直径に直径を３回かけた値」と折れる力の比はほぼ一定だということがわかった。直径が１ｍｍのときに折れる力は約　③　ｇ、直径が２ｍｍのときに折れる力は約　④　ｇである。
〔３〕長さ140ｍｍのブカティーニは約　Ｅ　ｇで折れる。ブカティーニの外径2.78ｍｍと同じ直径のスパゲッティの場合では、〔２〕で見つけた比が成り立つとして計算すると、約　Ｆ　ｇで折れるはずである。また、ブカティーニの断面の面積と同じ面積のスパゲッティの場合では、約　Ｇ　ｇで折れるはずである。これらのことから、ブカティーニが折れる力の強さは、　⑤　。

問６
栄一君が考えたことの文章が正しい内容になるように、空欄①、②を埋めなさい。

問７
栄一君が考えたことの文章が正しい内容になるように、空欄③、④にあてはまる最も近い数を、
それぞれ選びなさい。
③ア：７　イ：11　ウ：18　エ：33　オ：61
④ア：22　イ：55　ウ：100　エ：180　オ：4100

問８
栄一君が考えたことの文章が正しい内容になるように、空欄Ｅ～Ｇにあてはまる数を、
それぞれ四捨五入して10の倍数で答えなさい。

問９
栄一君が考えたことの文章が正しい内容になるように、空欄⑤にあてはまるものを選びなさい。
ア：同じ外径のスパゲッティより強い。
イ：同じ外径のスパゲッティと変わらない。
ウ：ブカティーニの内径と同じ値の直径のスパゲッティと変わらない
エ：断面の面積が同じスパゲッティと同じである
オ：同じ外径のブカティーニと比べると、内径が大きいほど強くなる
カ：同じ外径のスパゲッティと比べると、より少ない量の材料で同じ強さとなる
キ：同じ長さのスパゲッティと比べると、より少ない量の材料で同じ強さとなる
ク：長さや外径と無関係に、使われている材料の量が同じであれば同じ強さである

＠解説＠
【１】Ａ：ウ　Ｂ：ア　Ｃ：エ　Ｄ：イ

Ｂは稲穂。Ｄもススキとわかりやすい。
Ａはコムギ。Ｃのエノコログサはネコジャラシ。

【２】問１：ア、問２：ウ
体を動かすエネルギー源…炭水化物（デンプン）
体をつくる栄養素…タンパク質。遺伝子に基づいて合成される。
ちなみに、薄力粉と強力粉の違いはグルテンの量による。

【３】問１：247.5ｍｍ
平均の計算だけだが…１個ずつ計算すると大変(;`ω´)

247ｍｍが最も多いので、これを中央にして左右から集める。
246と248から15本ずつ減らし、中央の247に＋30本。

245と249から４本ずつ、244と250から２本ずつ、243と251から１本ずつを247ｍｍに集約。

今度は、248と250の５本ずつを249にまとめる。
247と249の25本ずつを248にまとめる。

243×１＋247×45＋248×54
…243を基準にすると、247＝243＋４、248＝243＋５
243を超えた部分を均し、あとで243を足す。
（４×45＋５×54）÷100＝4.5
243＋4.5＝247.5ｍｍ

＠別解＠
負の数を使ってもよいなら仮の平均がオススメです。
仮の平均を247ｍｍとする。
243＝247－４、244＝247－３、245＝247－２…
－４×２＋（－３）×２＋（－２）×４＋（－１）×15＋０×26＋１×24＋２×29＋３×７＋４×１
＝－８－６－８－15＋０＋24＋38＋21＋４
＝50ｍｍ
50ｍｍ÷100本＝0.5ｍｍ
最後に仮の平均と合算⇒247＋0.5＝247.5ｍｍ

問２：1.2倍
質量比だが、『成分が同じ』なので体積比で計算する。
また、『長さの平均も同じ』なので底面積の比でＯＫ。
底面積の比＝半径×半径の比＝直径×直径の比
問題文の最初に提示された数値を使おう！
1.68×1.68：1.85×1.85
＝2.82：3.42
＝141：171
171÷141＝1.21…→1.2倍

問３：下図参照
恒例のグラフ問題(;￣Д￣)ﾔﾀﾞｰ
表２を機械的に写す。

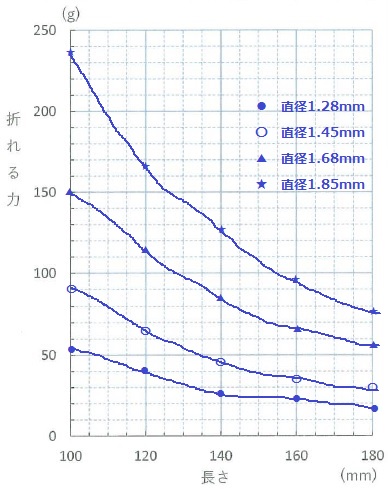
手が震えちゃった(´・д・｀)
プロットした座標の並びが直線っぽくないので、なめらかな曲線で描く。
色分けできないので、記号で凡例を記す。

問４：下図参照

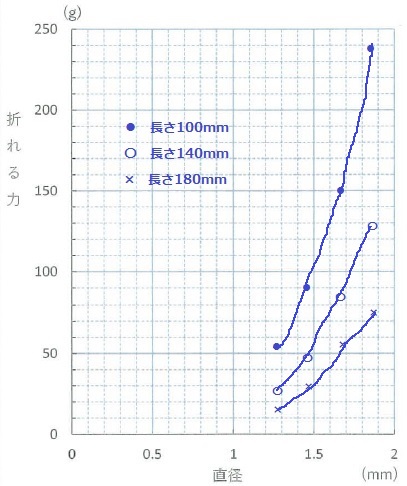
同様。今度は横軸が直径に変わる。
長さは100ｍｍ、140ｍｍ、180ｍｍのみ。
なめらかな曲線で描いてください。

問５：Ａ－2.07、Ｂ－257.6、Ｃ－247.5、Ｄ－82.5
文系にはツライ(；∀；)
『同じ長さで比べた場合、ブカティーニの重さは直径1.68ｍｍのスパゲッティの何倍か』
どの数値をもってくるべきか、散らかった情報を拾うのが難しい。
ブカティーニ１本の平均値は長さ257.6ｍｍ、重さが2.07ｇ。
直径1.68ｍｍのスパゲッティ１本の平均の長さは、問１より247.5ｍｍ。
長さ247.5ｍｍのブカ１本の重さを求める⇒2.07ｇ×247.5ｃｍ/257.6ｃｍ

問１の手前のにリード文より、直径1.68ｍｍのスパ100本の重さは82.5ｇ。
長さ247.5ｍｍ、直径1.68ｍｍのスパ１本の重さ⇒82.5÷100
これを先ほどの数値に割る。

↑まとめるとこんな感じ。
質量比なので、はじめは2.07ｇからスタート。

問６：①直径が太い方が大きく
②長さが短い方が大きい

グラフや表から明らか。
同じ長さだと直径が太い方が折れにくいので折れる力は大きい。
同じ太さだと長さが短い方が折れにくいので折れる力は大きい。

問７：③イ、④エ

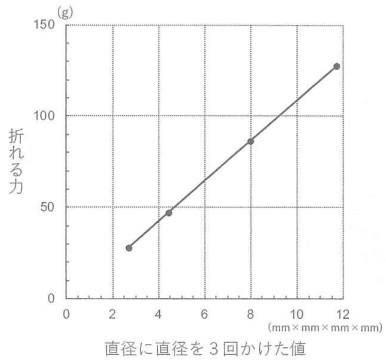
③直径１ｍｍの場合、１×１×１×１＝１
うえのグラフで、値が８のときに折れる力は80↑（80ちょっと上）。
１のときは10↑になるはず。
④直径２ｍｍの場合、２×２×２×２＝16
前問で値が１のときに折れる力が11だったので、11×16＝176ｇほど。

問８：Ｅ－570、Ｆ－660、Ｇ－500
Ｅ；表３より、140ｍｍのブカは570ｇで折れる。
Ｆ；『ブカの外径2.78ｍｍと同じ直径のスパ』→単純に直径2.78ｍｍのスパ。
最初の表より、2.78×2.78×2.78×2.78＝約59.7
前問③で値が１のときに折れる力は11ｇだったので、
11×59.7＝656.7≒660ｇ
*数値の取り扱いに気をつけよう！
前問④の選択肢180ｇで計算すると、180×59.7/16≒670ｇになってしまう。
直径×直径×直径×直径の値は「約～」と概数で表現される。
誤差を含むので、なるべく誤差の小さい値は直径×直径×直径×直径の値が小さいとき、
すなわち、直径が１ｍｍであるときを基準として計算する。

Ｇ；難所です。
ブカティーニの断面と同じ面積のスパゲッティを考える。
ブカの内径がどこにも出ていない(;`ω´)
ただ、問５で同じ長さの外径257.6ｍｍのブカの重さは、
直径1.68ｍｍのスパ１本の約2.4倍とあった。
質量比がブカ：スパ＝2.4：１
両者は同じ成分とみなすので、体積比も2.4：１
問５では同じ長さで算出したので、底面積の比も2.4：１
問２でみたように、底面積の比は直径×直径の比と同じ。
すなわち、直径×直径の比が2.4：１
直径の比＝（同じ数を２回かけると2.4になる数）：１
スパの直径①＝1.68ｍｍとすると、
ブカの断面を円形にしたときの直径〇2.4＝1.68×（同じ数を２回かけると2.4になる数）
〇2.4×〇2.4×〇2.4×〇2.4＝1.68×1.68×1.68×1.68×2.4×2.4
（２回の掛け算で2.4なので、４回の掛け算では2.4×2.4となる。数学でいえば〇2.4＝1.68×√2.4）

よって、折れる力は、
11×1.68×1.68×1.68×1.68×2.4×2.4
＝11×7.97×5.76＝504.9792≒500ｇ
(;´Д｀)ｷﾁｰ

問９：キ
８択もあるんですけど(;`ω´)
長さ140ｍｍ、同じ断面積でブカの折れる力は570ｇ、スパの折れる力は500ｇ。
ブカの方が折れにくい。
これを言い換えると、『ブカが折れる力の強さは、同じ長さのスパと比べると、
より少ない量の材料で（太さが細くても）同じ強さとなる』（キ）。

＠＠
元ネタが気になった調べてみました。どうやら材料力学という分野で、曲がりにくさを示す断面二次モーメントなるものがあるそうです。これによると、スパゲッティのような断面が円形の場合、断面二次モーメントはπｄ⁴/64。ｄが直径なので、変数ｄの４乗に比例します。ちなみに、ブカティーニのような中に空洞がある円形はπ（外径ｄ⁴－内径ｄ⁴）/64。大学レベルの物理学なので覚える必要性はゼロです。
難関中学（理科）解説ページに戻る