問題ＰＤＦ
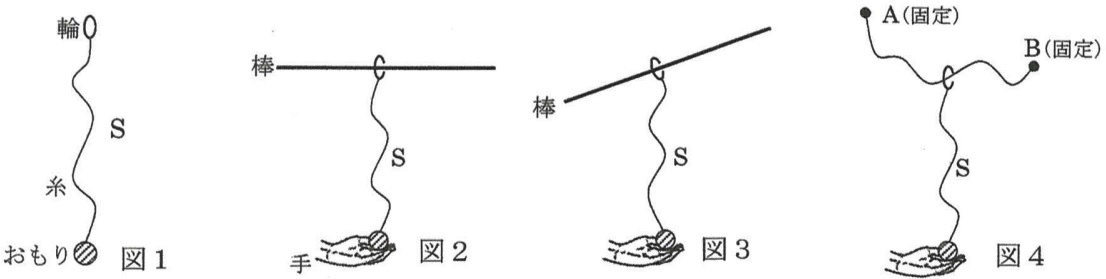図１のように、一本の糸の端に輪をくっつけて、もう一方の端におもりをくっつけたものを用意します（これをＳとよぶことにします）。図では輪とおもりは大きくえがいてありますが、それらの大きさは無視できるものとします。また、おもり以外の部分の重さはすべて無視するものとします。
図２のように、細くてかたい棒を水平に固定して、棒にＳの輪を通します。棒はじゅうぶん長く、輪と棒の間には摩擦はない（よくすべる）ものとします。おもりを持っていた手を放すと、輪がどの場所にあっても糸はつりあいます（安定して静止する）。
図３のように、棒をななめに固定した場合は、手を放したときにつりあう場所はありません。
図４のように、固定点Ａと固定点Ｂの間に別の糸をゆるく張り（点Ａのほうが点Ｂよりも高い位置にある）、その糸にＳの輪を通します。輪と糸の間には摩擦はないものとします。手を放すと、輪がすべって移動し、特定の場所でつりあいます。つりあっているときには糸はまっすぐになっている（たるんでいない）ことに注意して以下の問いに答えなさい。
問１
図４で手を放したあとでつりあったとき、輪の場所はどのような場所でしょうか。
最も適するものを選びなさい。
ア：ＡとＢを直線で結んだ真ん中の点の真下。
イ：アよりもＡに近いところ。 ウ：アよりもＢに近いところ。
問２
問１の場所の説明として適するものはどれですか。次のなかから選びなさい。
ア：輪から点Ａ、点Ｂまでの直線距離が等しい。 イ：輪から点Ａ、点Ｂまでの水平距離が等しい。
ウ：Ｓの糸の延長線が、張られた糸が折れ曲がって作る角を二等分する。
一端または両端に輪をつけた糸を新たに用意します（これをＳ’とよぶことにします）。
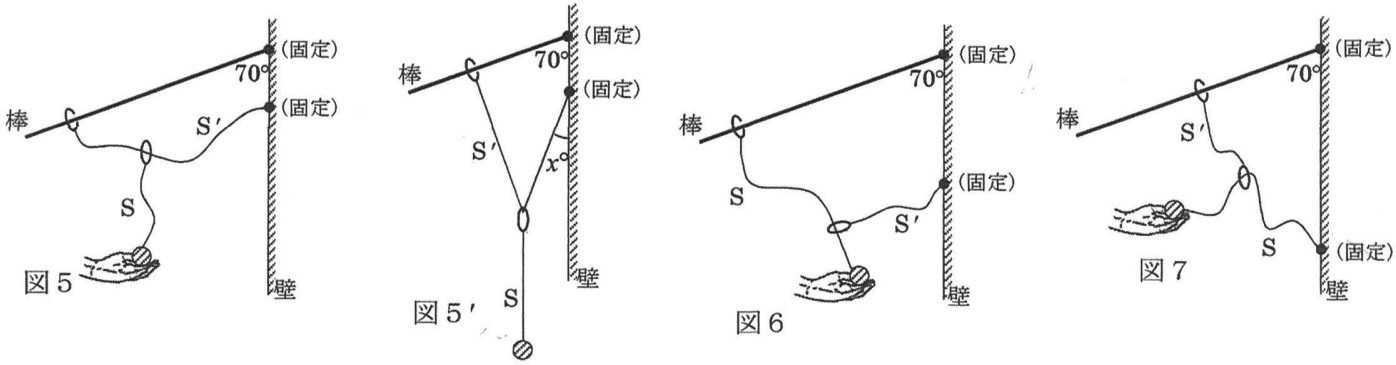
図５のように壁に棒を70度の角で固定します。
問３
図５に示したようにＳとＳ’を配置して手を放すと、ＳとＳ’は、およそ図５’のような形になってつりあいます。このときＳ’の糸が壁となす角度を答えなさい。（角度は壁の下方向となす角ｘの値で答えること。以下同様）
問４
図６のようにＳとＳ’を配置して手を放すと、ＳとＳ’はどのような形になってつりあうでしょうか。
Ｓ’の糸が壁となす角度を答えなさい。
問５
図７のようにＳとＳ’を配置して手を放すと、ＳとＳ’はどのような形になってつりあうでしょうか。
Ｓの糸が壁となす角度を答えなさい。
＠解説＠
問１：ウ
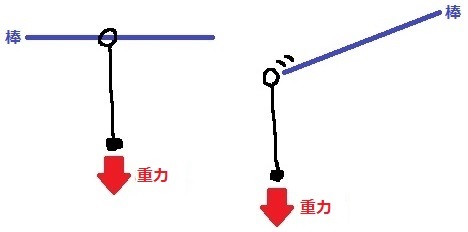
水平な棒だと、どこでも静止する。
傾いた棒だと静止する場所がなく、棒と輪の間の摩擦は考えないので、
おもりの重力にしたがって滑り落ちる。
たるんだ糸の場合は輪が動いて糸がＶ字に折れ曲がり、つりあって静止する。
仮にＡとＢが同じ高さにあったとすると、
左右対称となる糸の中点に落ち着くと予想できる。
Ａ側とＢ側から引っ張られる力の大きさはそれぞれ等しい。
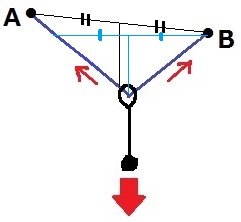
これはＡ側の長さを変えても同様である。
輪は真ん中よりもＢに近いところで落ち着く。
問２：ウ
後ろの設問に関わるので間違えられない。
左右対称に同じ力で引っ張られると判断できれば、
Ｓの糸の延長線が、張られた糸が作る角を２等分する。
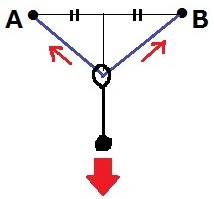
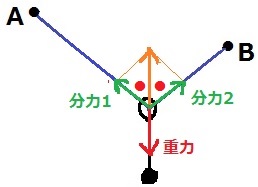
力の分解の作図方法は中学で習う。
力の方向は矢印の向き、力の大きさは矢印の長さで表す。
①輪から下におもりの重力に相応する矢印を描く。
②その一直線上の反対側に同じ長さの矢印を描く。
③矢印の先端を通過する、張られた糸に平行な線を描く。
④平行線と張られた糸の交点までが分解された力（分力）で、
上図では分力１と分力２の大きさが等しい。
問３：20°
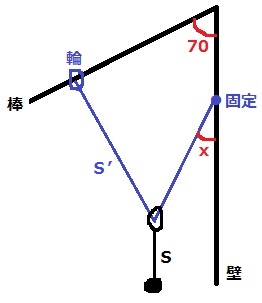
ポイントは、Ｓ’につけた輪は棒のどこで止まるのか。
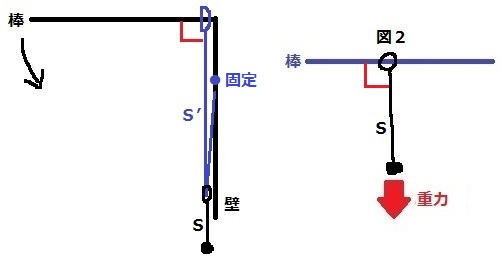
もし、棒が壁に対して90°であった場合を考える。
おもりは壁の固定点に引き寄せられ、輪は右側に移動して壁に密着し、
図２と同じく棒と糸Ｓ’は垂直になる。
棒を下に傾けたとしても、棒と糸Ｓ’が垂直である関係が維持されるのでは？
ようするに糸Ｓ’が引っ張られる方向に対して輪が向き、糸と棒が垂直になるところで輪が止まる。
ここに気付けるかどうか。
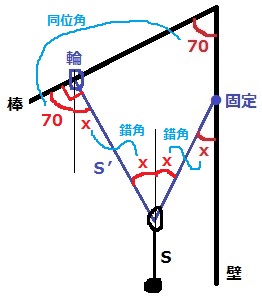
２つの輪を通る、壁に対して平行な線をひく。
ｘを錯角→等角（糸がつくる角の二等分線）→錯角で移し、70°を同位角で移す。
棒とＳ’の角度は90°なので、ｘ＝90－70＝20°
問４：80°
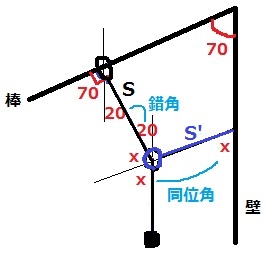
Ｓ’の一方を壁に固定する。
Ｓ’を反対側へ延長。20°を錯角、ｘを同位角で移す。
等角（糸がつくる角の二等分線）よりｘが２つ。
一直線に注目して、ｘ＝（180－20）÷２＝80°
問５：140°
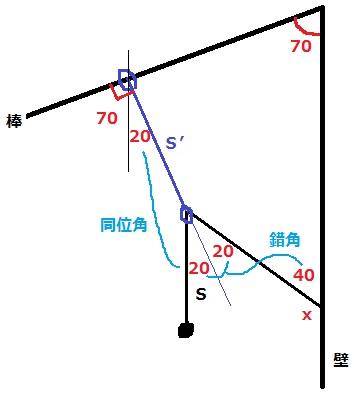
今度はＳの一方を壁に固定して、Ｓ’の両端に輪をつける。
Ｓ’を延長して、20°を同位角で移動。
等角の和40°を錯角で移動。
ｘ＝180－40＝140°
難関中学（理科）解説ページに戻る
コメント