2020年度　岡山県公立高校入試過去問【数学】解説

平均56.6点（前年比；－4.1点）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

①
４＋（－８）
＝４－８＝－４

②
（－18）÷（－３）
＝６

③
４（２ａ－ｂ）－（－３ａ＋ｂ）
＝８ａ－４ｂ＋３ａ－ｂ
＝11ａ－５ｂ

④
６ａｂ×（－３/２ａ）
＝－９ａ²ｂ

⑤
（１－√５）²
＝１－２√５＋５
＝６－２√５

⑥
ｘ²－ｘ－３＝０
因数分解ができないので解の公式。
ｘ＝（１±√13）/２

⑦

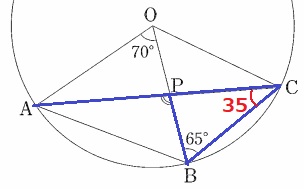
円周角定理より、∠ＡＣＢ＝70÷２＝35°
△ＢＣＰで外角定理→∠ＡＰＢ＝35＋65＝100°

⑧
３枚の硬貨を投げて表・裏がでる結果→２³＝８通り
すべて裏がでる→１通り
少なくとも１枚は表→８－１＝７通り
７/８

⑨
円柱の体積…ｒ×ｒ×π×２ｒ＝２πｒ³
球の体積…４/３πｒ³
２πｒ³÷４/３πｒ³＝３/２倍
ア
*本問は選択肢問題なのでありがたいが、分母分子を逆にしないように！
球の何倍かだから、球の体積が分母（割る数）にくる。

⑩（１）
相対度数は小数で求める。
３÷15＝0.20

（２）
階級値×度数を足して総和を求め、それを15で割る。
（10×０+30×１+50×６+70×４+90×３＋110×１）÷15
＝990÷15＝66点

大問２（標本調査・方程式）

①
無作為に取り出した25個のうち、模様入り：単色＝６：19
全体は500個なので、６×500/25＝120
イ

②（１）
個数と値段で連立。
ｘ＋ｙ＝500　…①
７ｘ＋３ｙ＝2000　…②

（２）
うえの連立を解く。
②－①×３
７ｘ＋３ｙ＝2000
－)３ｘ＋３ｙ＝1500
４ｘ　　　＝500
ｘ＝125
①に代入、ｙ＝500－125＝375
模様入り…125個、単色…375個

大問３（関数）

①
ア：ａ＞０の比例。右上のグラフで、ｘが増加すればｙも増加する。〇
イ：ａ＜０の一次関数。右下のグラフで、ｘが増加すればｙは減少。×
ウ：ａ＞０の反比例。双曲線を描き、ｘが増加すればｙは減少。×
エ：ａ＜０の放物線。上に凸のグラフで、ｘ＝－３のときｙ＝－９
ｘ＝１のとき、ｙ＝－１で、ｙの値は増加する。〇

ア・エ

②（１）
変化の割合からａを求める。
ｙ＝ａｘ²より、ｘ＝－２のとき、ｙ＝４ａ
ｘ＝４のとき、ｙ＝16ａ
16ａ

（２）
続き。
答案では過程も記述する。
変化の割合＝（ｙの増加量）/（ｘの増加量）
（16ａ－４ａ）/｛４－（－２）｝
＝12ａ/６＝２ａ＝１
ａ＝１/２

③
ｙ＝１/２ｘ²にｘ＝－２を代入。
Ａ（－２、２）
変化の割合は１ということは斜め45度。

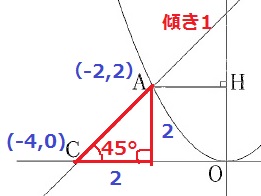
直角二等辺三角形を作成。
Ａから下に２、左に２で、Ｃ（－４、０）
－４

④（１）

ＯＨを回転の軸として台形ＯＨＡＣをグルっと回すと円錐台になる。
△ＩＡＨ∽△ＩＣＯで、ともに直角三角形。ＩＯ＝４ｃｍ
大きい円錐から上の小さい円錐を引く。
辺の比１：２→体積比１：８
小さい円錐の体積を【１】とすると、円錐台の体積は【７】
４×４×π×４÷３×７/８＝56/３πｃｍ³

（２）
今度は表面積を求める。
上と下は円。２×２×π＋４×４×π＝20πｃｍ²
問題は側面積。
△ＩＣＯは１：１：√２の直角三角形→ＩＣ＝４√２

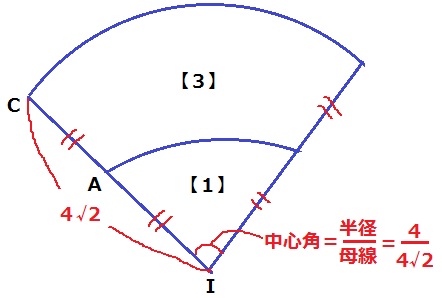
中心角は〔＝×半径/母線〕で処理。
辺の比１：２→面積比１：４から、求積すべき範囲は【３】
４√２×４√２×π×４/４√２×３/４＝12√２πｃｍ²
したがって、20π＋12√２π＝（20＋12√２）πｃｍ²

大問４（文章題）

①
垂線の作図。
教科書通りの作図なので必答。
１：Ａに針を合わせて弧を描く。
２：ℓとの交点から弧を２つ描く。
３：その交点とＡを結ぶ。

②
ＯＡ：ＡＢ＝４：５だから、
ＡＢ＝12×５/４＝15ｍ

③（１）
ＯＣ：ＣＤ＝２：３
ＯＤは右に２、上に３なので、傾きは３/２。
ＯＤ；ｙ＝３/２ｘ
３/２ｘ

（２）

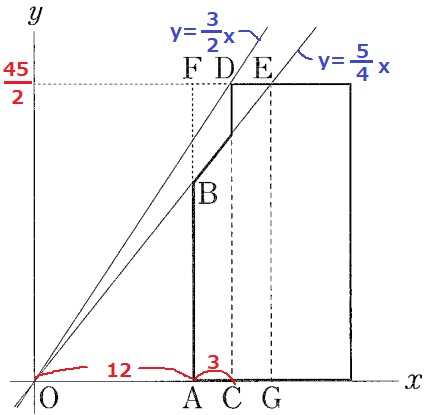
ｙ＝３/２ｘにｘ＝15を代入し、Ｄのｙ座標を求める。
ｙ＝３/２×15＝45/２

（３）
点Ｅのｘ座標を求める過程を書く。
Ｅのｙ座標が45/２なので、これをｙ＝５/４ｘに代入。
45/２＝５/４ｘ
ｘ＝18
点Ｅのｘ座標は18。

④
『図３をもとに図４を作成』とあるので、数値は先ほどの図を用いる。

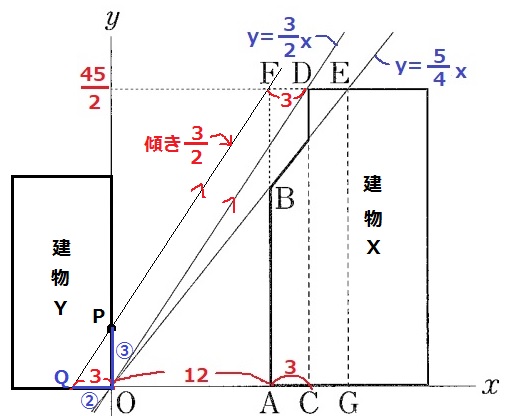
ＦＰとｘ軸との交点をＱとする。
四角形ＦＱＯＤは２組の対辺が平行な平行四辺形。
ＱＯ＝ＦＤ＝３ｍ
ＱＦの傾きはＯＤと同じ３/２だから、ＱＯ：ＯＰ＝２：３
ＯＰ＝３×３/２＝９/２ｍ

＠日照権＠
太陽の光を享受する権利を日照権という。日照権を明文化した法律はないが、建築基準法では本問のような斜線制限や日影規制の定めにより、最低限度の採光を確保する仕組みはとられている。
また、建築制限に違反していなくても、社会通念上受任すべき限度を超えた場合（受忍限度論）も損害賠償請求や建築差止め請求ができる可能性はある。しかし、よほど酷い場合でないと難しいそうです。

大問５（平面図形）

①
平行四辺形になる条件
１；２組の対辺が平行である。
２；２組の対辺の長さが等しい。（エ）
３；２組の対角の大きさが等しい。
４；対角線が各々の中点で交わる。（イ）
５；１組の対辺が平行で、かつ長さが等しい。（ア）

対角線の長さが等しく、垂直に交じっても平行四辺形とは限らない。
ウ

②（１）
△ＡＦＥ∽△ＢＦＧの証明。

ＡＥ//ＢＧから、同位角で∠ＥＡＦ＝ＧＢＦ
共通角より、∠ＡＦＥ＝∠ＢＦＧ
２角が等しいので∽。
*書きやすいので証明が苦手な人も正解したい。

（２）
ＢがＡＦの中点→△ＡＦＥと△ＢＦＧの辺の比は１：２。
ＢＧ＝１/２ＡＥ
１/２
*ＡＥ＝②とすると、ＢＧ＝ＥＤ＝①となり、ＢＧ＝ＥＤとなる。

③（１）
ＤＥ＝15×１/３＝５ｃｍ
△ＤＥＨの底辺ＤＥ、高さがＨＰなので、△ＤＥＨの面積が知りたい。

前問でＢＧ＝ＥＤであった。
ＡＤ//ＢＣの錯角から、１辺と両端角相等より△ＢＧＨ≡△ＤＥＨ
ＤＨ＝ＥＨ＝ＢＨ＝ＧＨ

Ｈを通るＡＤに平行な線を引き、ＡＢとの交点をＩとする。
Ｈは対角線ＢＤの中点。△ＡＢＤ∽△ＩＢＨよりＡＩ：ＩＢ＝１：１
△ＢＧＨを△ＢＧＩに等積変形。
△ＢＧＩと△ＢＧＦの面積比→ＩＢ：ＢＦ＝１：２
指針；【△ＢＧＦ⇒△ＢＧＩ＝△ＢＧＨ＝△ＤＥＨ】
△ＢＧＩ（△ＤＥＨ）の面積は、20√６×１/２＝10√６ｃｍ²
よって、ＰＨは、10√６×２÷５＝４√６ｃｍ

（２）

ＰＨを延長し、ＢＣとの交点をＱとする。
ＰＨもＨＱは合同な二等辺三角形の高さ→ＰＨ＝ＨＱ
ＰＱ＝４√６×２＝８√６ｃｍ

二等辺の頂角から底辺におろした垂線は底辺の中点を通る＋合同な二等辺→ＰＥ＝ＱＢ
つまり、ＰＱを下方向に平行移動させるとＢＥになる。
△ＡＢＥで三平方。
ＡＢ²＝10²＋（８√６）²＝100＋384＝484
ＡＢ＝22ｃｍ