問題PDF
2種類の昆虫AとBを考えます。昆虫AとBは、卵から出た1齢幼虫が成長と脱皮をくり返し、2齢幼虫、3齢幼虫を経て4齢幼虫になります。成長した4齢幼虫は脱皮、変態してさなぎになります。さなぎは脱皮して成虫になります。

卵から成虫になれる個体はごくわずかで、昆虫AとBでは、成長してそれぞれの段階へ進める個体の割合が異なります。
表1は、昆虫AとBが10000個の卵からスタートして、自然界で段階ごとに数を減らしていくようすです。表1の個体数とは、各段階での初期個体数を示しています。例えば昆虫Aでは10000個のうち、卵の段階で1665個が死亡し、8335個体が1齢幼虫になれました。また、2齢幼虫の段階で表1の(ア)の数が死亡し、5005個体が3齢幼虫になれました。同様に昆虫Bでは、卵の段階で表1の(ウ)の数が死亡し、1齢幼虫になれたのは3000個体です。
表1の死亡率とは、ある段階まで成長できた個体のうち、その段階で死亡する個体の割合を(%)で示したものです。例えば昆虫Aでは卵の段階での死亡率は![]() で整数では17%です。
で整数では17%です。

(1)
次の( )を適切に補いなさい。
昆虫の卵から幼虫が出てくることを( ① )と言います。
また、幼虫やさなぎが脱皮、変態して成虫に変わることを( ② )と言います。
(2)
表1の(ア)~(カ)を整数で答えなさい。
図1は段階ごとの変化を見るために、表1の個体数を折れ線で結んだグラフです。
昆虫AとBでは、個体数の減り方が異なることがわかります。

図1の場合、縦軸の目盛りは均等な間隔で、同じ目盛り分なら、長さも同じです。例えば、10目盛り上がるときの長さはどこでも同じで、1000ずつ数が大きくなります。図1の縦軸は、長さで数の差を表しています。
次に、図2のようなグラフを作ると、図1とは異なる特徴をグラフから見つけることができます。図2は、縦軸の目盛りが図1と異なります。

(3)
図2について、次の( )に適する数を答えなさい。
図2は、縦軸の目盛り幅が均等ではありません。一番下の目盛りは1です。1から10までと10から100、100から1000、1000から10000までが同じ長さになっています。
1の1つ上の目盛りが2、その上が3です。10の1つの上が20、その次が30です。100の1つ上が200、その次が300です。1000の1つ上が2000、その次が3000です。
例えば、1から10まで、2から20まで、600から( あ )までが同じ長さで作られていて、( い )目盛り上がるごとに、もとの数の10倍になります。反対に、一番上の10000に1/10を( う )回かけると、一番下の1になります。
1から2までと、2から4までは、目盛りの数は異なりますが、長さは同じです。4から8まで、( え )から10000までの長さも1から2までの長さと同じです。10から30までの長さは、30から90までの長さや200から( お )までの長さと同じです。2000から400までの長さは、50から( か )までの長さと同じです。
図2の縦軸は、長さの違いで、何倍の違いなのか、何分の1の違いなのか、を表すことができます。
図1と同じ印を使って、図2に昆虫AとBの個体数を書き込むと図3のようになります。
ただし、次の(サ)~(ス)の点は記されていません。
(サ)Aの成虫 (シ)Bの1齢幼虫 (ス)Bの2齢幼虫
(4)
図3の(サ)~(ス)の個体数を、図1と同じ印で記入し、(サ)~(ス)の記号を書き入れなさい。

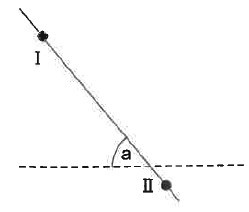
下のような2つの点ⅠとⅡを通る、右上がりの直線を引きます。直線とグラフの横軸とのなす角aの大きさを、直線の傾き角と呼ぶことにします。
図1と図3では、グラフにおける傾き角が持つ意味が異なります。
(5)
次の〔 〕に適するものを○で囲みなさい。
図1では、昆虫①〔A・B〕において各段階の傾き角がほぼ等しい。
図3では、昆虫②〔A・B〕において各段階の傾き角がほぼ等しい。
表1から、昆虫Aは各段階での③〔死亡数・死亡率〕が等しく、昆虫Bは各段階での④〔死亡数・死亡率〕が等しいことがわかる。また、死亡数に注目すると、1齢幼虫における死亡数が多いのは昆虫⑤〔A・B〕である。死亡率に注目すると、さなぎにおける死亡率が大きいのは昆虫⑥〔A・B〕である。
図1では、グラフの傾き角から⑦〔死亡数・死亡率〕の違いがわかり、図3ではグラフの傾き角から⑧〔死亡数・死亡率〕の違いがわかる。
上の昆虫AとBは実在しない昆虫ですが、次に実在する昆虫Cについて考えます。
昆虫Cはガの仲間で、サクラやヤナギの葉を食べる害虫として知られています。昆虫Cの幼虫は脱皮をくり返して7齢幼虫まで成長し、さなぎを経て成虫になります。卵から出た幼虫は糸を吐いて網状の巣を作り、集団で生活します。その後、ある齢の幼虫になると単独で生活をするようになります。単独での生活を始めると、他の昆虫や鳥に食われるので、急に死亡率が大きくなります。
ある年、昆虫Cの4287個の卵について、自然の状態での成長を追跡しました。
図4に各段階での個体数を示します。

(6)
図4から昆虫Cについて考えられることとして、〔 〕に適するものを○で囲み、( )を適切に補いなさい。
7齢幼虫とさなぎを比較すると、死亡数が多いのは①〔7齢幼虫・さなぎ〕の段階である。また、死亡率が大きいのは②〔7齢幼虫・さなぎ〕の段階である。さなぎまでの各段階のうち、最も死亡率が小さいのは( ③ )の段階である。巣での集団生活をやめて単独での生活を始めるのは、( ④ )齢幼虫だと考えられる。
@解説@
(1)①孵化、②羽化
孵化…卵からかえること。
羽化…昆虫の幼虫やさなぎが成虫になること。
(2)ア…1665、イ…25、ウ…7000、エ…70、オ…630、カ…70

ア…6670-5005=1665
イ…1665÷6670×100=24.9…≒25
ウ…10000-3000=7000
エ…7000÷10000×100=70
オ…900-270=630
カ…630÷900×100=70
(3)あ…6000、い…9、う…4、え…5000、お…600、か…10
受験生の大半は見たことがない目盛りなので、現場で考えるしかない。
『1~10』『10~100』『100~1000』『1000~10000』の長さが同じ。
桁ごとで周期的に長さが等しい。
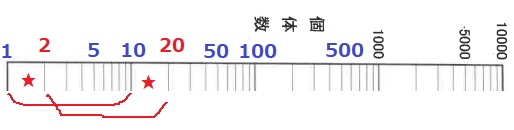
『1~10』『2~20』が同じ。
(共通する2~10の両サイドの★が同じ長さ)
ここから、同じ桁のなかでは左から〇番目の目盛りの幅が等しいのでは?と推測する。
(1~2=10~20=100~200、2~3=20~30=200~300など)
桁ごとに(10倍ごとに)目盛りの幅が周期的だから、
1~10、2~20と、600~6000が等しくなる(あ)
はじめが1で1~10までの目盛りの数は9個。
10~100までの目盛りも9個→9目盛り上がるごとに10倍(い)
10000に1/10を何回かけると1になるか?→4回(う)
『1~2』『2~4』までの長さが同じ。
値が2倍になれば長さが等しくなると推測する→『5000~10000』(え)
『10~30』『30~90』が同じ。
値が3倍なので、『200~600』(お)
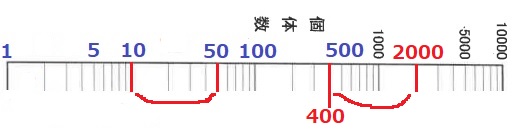
2000÷400=5なので、50÷5=10(か)
*割合がポイント!
うしろの設問にある『死亡率』がヒントになる。
@対数グラフ@
対数目盛りでは目盛りの幅が10のベキ乗(10・100・1000…)で等しい。
1目盛りの幅は等間隔ではなく、縦軸に0がない。
対数とは、高2で習う常用対数(log)のこと。
極端な数値をもつデータがあるとき、普通の目盛りでは他のデータが見づらくなってしまうが、
対数グラフを使うとデータ間の差がわかりやすくなる。


左が通常のグラフ、右が対数グラフで太陽系の天体の大きさを示す。
太陽が大きすぎて他がどっこいどっこいだが、対数グラフでは大きさの順位が把握しやすい。
(4)

横軸と縦軸に気を付けて、表1からプロットする。
(サ)Aの成虫:10匹(シ)Bの1齢幼虫:3000匹(ス)Bの2齢幼虫:900匹
今年の理科は合格者平均が7割5分だったので、ここは取りこぼせない。
(5)①A②B③死亡数④死亡率⑤B⑥A⑦死亡数⑧死亡率
内容をきちんと理解すれば、一貫して解答できる。


左の図1ではA、右の図3ではBが直線(①・②)
図1は目盛りが等間隔なので、Aは各段階での死亡数が等しい(③)
図3は割合に応じて目盛りの幅を変えたので、Bは各段階での死亡率が等しい(④)
1齢幼虫の死亡数が多いのは、図1(または表1)よりB(⑤)
さなぎの死亡率が多いのは、図3よりA(⑥)
図1では死亡数、図3では死亡率の違いがわかる(⑦・⑧)
(6)①7齢幼虫②7齢幼虫③卵④4

7齢幼虫の死亡数…40-13(くらい)=27匹
さなぎの死亡数…13-7=6匹 7齢幼虫の方が多い(①)
7齢幼虫の死亡率…27/40、さなぎの死亡率…6/13だが、
計算せずとも対数目盛りから傾き角の大きい7齢幼虫の方が死亡率が高い(②)
死亡率が最も少ない段階は、傾き角が小さい卵(③)
リード文より『単独生活を始めて急に死亡率が大きくなる』とあるので、
単独生活をはじめるのは、傾き角が大きくなる4齢幼虫と考えられる(④)
@生存曲線@

Wikibooksより。縦軸の生存個体数はあくまで相対値であり、相対年齢0(誕生)のときを〔1000〕、
相対年齢100(死滅)を〔1〕(1でなくてもOK)としたときの割合。
(1000匹から100匹に減るではないので注意!)
生存曲線は3つのタイプに分かれる。
A:晩死型…幼齢期の死亡率が低い。
親の保護を受けて育つ哺乳類やアリやミツバチなどの社会性昆虫。
B:平均型…各年齢を通じて死亡率がほぼ一定。
小型の哺乳類や鳥類、爬虫類。入試ではヒドラが狙われやすい。

ヒドラは無性生殖(オスとメスが交配しない)の1つである出芽の代表格。
親の体の一部から子供がニョキッと出てくる。
C:早死型…親の保護を受けず、幼齢の死亡率が高い。
魚類は多量の卵を生むことで子孫を残す(数打ちゃあたる戦法)


コメント