2020年度　香川県公立高校入試問題過去問【数学】解説

平均28.4点（50点満点、前年比；＋1.2点）
問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）
10÷（－２）＋４
＝－５＋４＝－１

（２）
ａ²－４
＝（－３）²－４
＝９－４＝５

（３）
９×（２ｘ－１）/３　←９と３で約分
＝３×（２ｘ－１）
＝６ｘ－３

（４）
（ｘ－１）：ｘ＝３：５
内項と外項の積で、
３ｘ＝５（ｘ－１）
ｘ＝５/２

（５）
（３√２＋１）（３√２－１）
＝（３√２）²－１²
＝18－１＝17

（６）
ｘ（ｘ＋１）－３（ｘ＋５）
＝ｘ²＋ｘ－３ｘ－15
＝ｘ²－２ｘ－15
＝（ｘ－５）（ｘ＋３）

（７）
√180＝６√５
ａ＝５を代入すれば、６×√５×√５＝30でルートを外せる。
ａ＝５

大問２（小問集合）

（１）

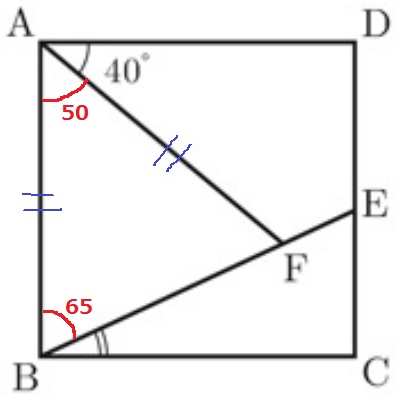
∠ＢＡＦ＝90－40＝50°
△ＡＢＦは二等辺ゆえ、∠ＡＢＦ＝（180－50）÷２＝65°
∠ＥＢＣ＝90－65＝25°

（２）ア
ネジレ→平行ではない、かつ延長しても交わらない。
辺ＤＦ（イ）

イ
△ＡＢＣの面積は、６×３÷２＝９ｃｍ²
ＰＡは三角錐Ｐ－ＡＢＣの高さにあたるので、
ＰＡ＝15×３÷９＝５ｃｍ
△ＰＡＢで三平方→ＰＢ＝√61ｃｍ

（３）
中学入試の算数みたいな問題。

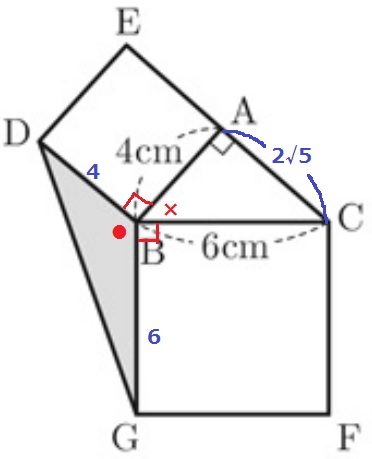
△ＡＢＣで三平方→ＡＣ＝２√５ｃｍ
△ＡＢＣは直角二等辺にみえるけど違うので注意！
幾何の鉄則、困ったら角度の調査。
Ｂに目をやると、正方形の内角が２つ集合しているので、●＋×＝180°
ＤＢ＝ＡＢなので…

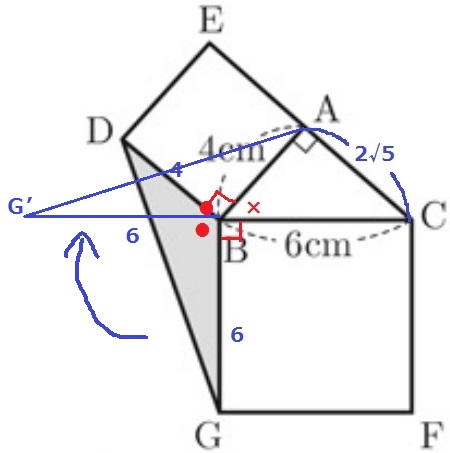
Ｂを中心に△ＢＤＧを時計回りに回転させる。
すると、DがAに接し、●＋×＝180°からＧ’―Ｂ―Ｃが一直線になる！
△ＡＢＧ’と△ＡＢＣは底辺が６ｃｍで高さが共通だから面積が一緒。
つまり、△ＡＢＣの面積が答えになる。
２√５×４÷２＝４√５ｃｍ²

大問３（小問集合２）

（１）
積が９以下を調べる。
◆Ａが１
Ｂは１～６の６通り。
Ａ・Ｂの逆を含めると、６×２－１＝11通り。
*（１、１）は含まないので－１をしている。

◆Ａが２
１は検討済みだから、Ｂは２～４の３通り。
逆を含めて、３×２－１＝５通り
*（２、２）を除外して－１。

◆Ａが３
（３、３）のみ。
計17通り。
確率は、17/36。

（２）
最頻値（モード）は最もあらわれている値。
10～20分の階級の階級値で答える。
２つの平均で15分。

（３）ア
ｘ＝１のとき、ｙ＝１
ｘ＝４のとき、ｙ＝16
変化の割合＝（ｙの増加量）/（ｘの増加量）
＝（16－１）/（４－１）＝５

＠別解＠
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
１×（１＋４）＝５

イ

ｙ＝１/２ｘ²にｘ＝－４を代入。Ａ（－４、８）
ＡＢ：ＢＣ＝２：１より、Ｃのｘ座標は２。
ｙ＝ｘ²に代入して、Ｃ（２、４）
Ａ（－４、８）→Ｃ（２、４）
右に６、下に４だから、傾きは－４/６＝－２/３

ｙ＝－２/３ｘ＋ｂに、Ｃ（２、４）を放り込む。
４＝－２/３×２＋ｂ
ｂ＝16/３
ｙ＝－２/３ｘ＋16/３

（４）
答案では求める過程も記述する。
バレー部の部員全員をｘ人し、利用料金で等式を立てる。
当初の予定では、250ｘ円。
しかし、３人欠席してｘ－３人となり、１人あたり280円集めて120円余った。
⇒280（ｘ－３）－120円。
*余ったから、集金した金額から120円引かないと利用料金にならない。
250ｘ＝280（ｘ－３）－120
ｘ＝32

大問４（規則・数量変化）

（１）ア

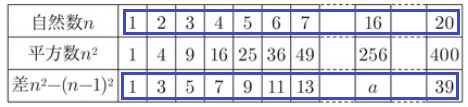
上と下を見ると規則が見つかる。
ようは、16番目の奇数は何かということ。
ａ＝16×２－１＝31

イ
２ｎ－１＝49
ｎ＝25
ｎ－１＝24
ｎ²－（ｎ－１）²＝２ｎ－１が49のときを考えているので、
25²－24²の値は49の正の平方根である７。
７、24、25

＠余談＠

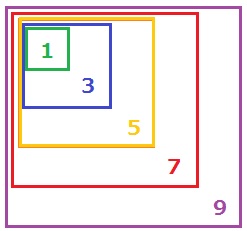
なぜ、連続する数の平方数の差が奇数になるのか。
正方形を並べて重ならない部分をみるとわかりやすい。

（２）ア
Ｐは使わない。

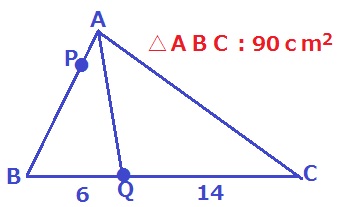
３秒後、ＱはＢから６ｃｍ移動している。
ＢＱ：ＱＣ＝６：14＝３：７
△ＡＢＱの面積は、90×３/10＝27ｃｍ²

イ

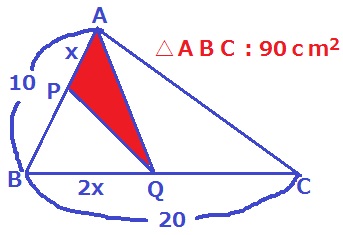
【方針；△ＡＢＣ⇒△ＡＢＱ⇒△ＡＰＱ】
90×２ｘ/20×ｘ/10＝９/10ｘ²ｃｍ²

ウ
答案では求める過程も記述する。
前問より、ｘ秒後の△ＡＰＱの面積は９/10ｘ²。
この３倍が、ｘ＋１秒後の△ＡＰＱの面積である９/10（ｘ＋１）²に等しい。
９/10ｘ²×３＝９/10（ｘ＋１）²　←両辺から９/10を除外
３ｘ²＝ｘ²＋２ｘ＋１
２ｘ²－２ｘ－１＝０
因数分解ができないので解の公式を適用。
ｂの係数が偶数なのでｂ＝２ｂ’が使える。
０＜ｘ≦９より、ｘ＝（１＋√３）/２

大問５（図形の証明）

（１）
△ＡＧＯ∽△ＡＦＢの証明。

共通角●。
仮定より、∠ＡＧＯ＝90°
半円の弧に対する円周角で、∠ＡＦＢ＝90°
以上、２角が等しく∽。

（２）
△ＡＢＣ≡△ＡＨＤの証明。

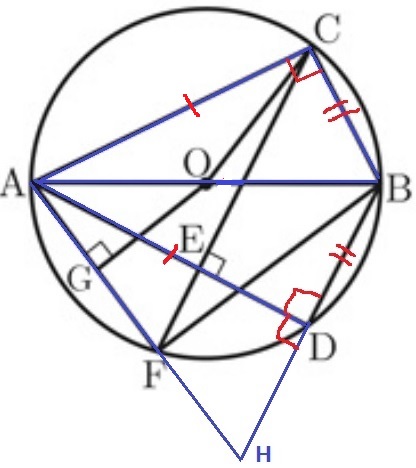
△ＡＢＣと△ＡＨＤが離れている(´ﾟωﾟ`;)
ＢＣ＝ＢＤをまだ使ってない。
半円の弧に対する円周角で、∠ＡＣＢ＝∠ＡＤＢ＝90°
共通辺ＡＢと組み合わせ、斜辺と他の１辺が等しい直角三角形で△ＡＢＣ≡△ＡＢＤ
ＡＣ＝ＡＤ

∠ＡＤＨ＝180－90＝90°
もう１つの等角が欲しい。ここからどうするか…。
ごちゃごちゃした図形なので迷子になりやすい。
円外の情報は不足しているので、∠ＡＨＤより∠ＨＡＤをなんとか求めたい。

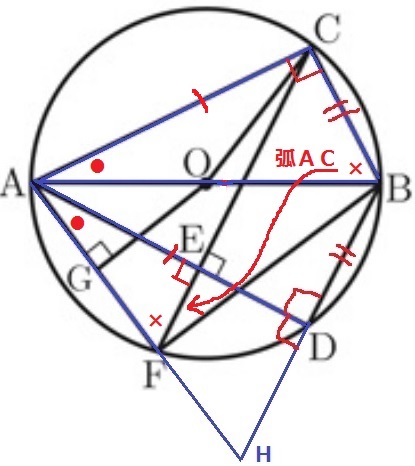
∠ＣＡＢ＝●、∠ＣＢＡ＝×とおく。
●＋×＝90°
弧ＡＣに対する円周角で、∠ＡＦＥ＝×
対頂角で∠ＡＥＦ＝90°だから、△ＡＥＦの残りの内角である∠ＥＡＦ＝180－90－×＝●
一辺両端角が等しく、合同となる。

平均が６割に近く、基本問題は落としたくない。
大問２
（３）中学入試っぽい問題は正答率がガクッと下がる傾向にある。
図形の回転移動は初見ではかなり厳しい。
大問３
（１）表を書いて調べてもいい。
大問４
ここから差がつきやすい。
（１）25²－24²は計算しない。
（２）図を描くこと。ｘの１秒後はｘ＋１。
大問５
（２）ＡＤとＣＦが直交するＥがポイントではないかと思われる。
完全解答はできなくても部分点をとれれば及第点〇。
公立高校入試解説ページに戻る