問題PDF
いくつかの駅を線路でつなぎます。
下のルールにしたがって、駅を線路でつなぐとき、全部で何通りのつなぎ方があるか考えます。
ただし、どの駅とどの駅とが線路でつながれているかでつなぎ方を区別するものとします。
たとえば、図1のような駅のつなぎ方は同じものとみなします。
【ルール】
・すべての駅を線路が交差しないようにつなぐ。
・輪ができないように線路でつなぐ。
たとえば、図2のような線路のつなぎ方はA駅とB駅とC駅で輪になっているので、考えません。
・1つの駅といくつかの駅とを線路でつないでよいものとします。

(1)
図あのようなA駅、B駅、C駅の3つの駅を線路でつなぐとき、
つなぎ方は全部で何通りありますか。
(2)
図いのようなA駅、B駅、C駅、D駅の4つの駅を線路でつなぐとき、
1つの駅から3つの駅へ線路でつなぐつなぎ方は全部で何通りありますか。
(3)
図いのようなA駅、B駅、C駅、D駅の4つの駅を線路でつなぐとき、
つなぎ方は全部で何通りありますか。
(4)
図うのようなA駅、B駅、C駅、D駅、E駅の5つの駅を線路でつなぐとき、
つなぎ方は全部で何通りありますか。
@解説@
(1)

3駅をつなぐには、串団子しかない。
注意すべきは、左右を入れ替えても同じつなぎ方になってしまうこと。
『どの駅とどの駅とが線路でつながれているか』で区別するので、
左から順に〔A・B・C〕も〔C・B・A〕も同じ。
つまるところ、真ん中を何にするかで3通りとなる。
(2)

ハブ空港スタイル。回転してもつなぎ方は同じ。
これも真ん中を何にするかで4通り。
(3)
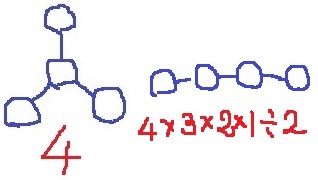
4駅をつなぐには、ハブ空港か串団子。
前問からハブ空港は4通り。
串団子は4つの順列から左右入れ替えても同じなので、
4×3×2×1÷2=12通り
計16通り
(4)
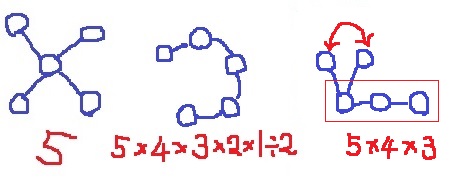
5駅つなぐには、ハブ空港か串団子かアリ。
前問と考えは同様。
ハブ空港は真ん中をどうするか→5通り
串団子は、5×4×3×2×1÷2=60通り
アリは胴体部分の3つを順列→5×4×3=60通り
触角は左右入れ替えても同じ。
また、お団子と違って左右対称ではないので÷2をしない。
計125通り



コメント