問題PDF
3本の針がある新しい時計をつくりました。図の●は、2つの点線の円周をそれぞれ等分していて、すべての針は時計回りにそれぞれ一定の速さで回転しつづけます。針を短い順にA、B、Cとするとき、針が一周するのにかかる時間は、Aは8時間、Bは3時間、Cは1時間です。午前0時ちょうどに、すべての針は数字の0を指しています。次の問いに答えなさい。ただし、解答らんには、【例】のように24時間表記に直した時刻を答えるものとします。
【例】午前10時30分→「10時30分」、午後6時→「18時」
(1)
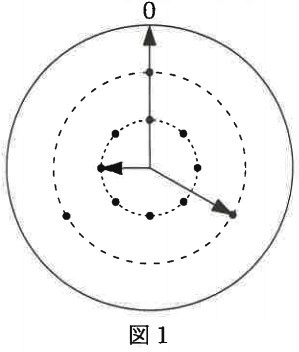
図1では、針Cが数字の0を指しています。
この時刻は何時ちょうどですか。
(2)
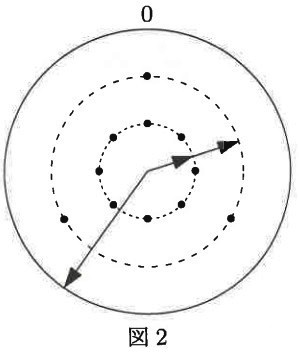
図2では、針Aと針Bが重なっています。
この時刻は何時何分ですか。
(3)
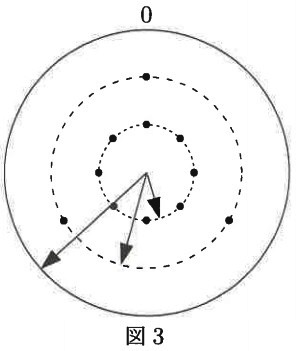
図3では、針Aと針Cでつくられる角を針Bが2等分しています。
この時刻は何時何分ですか。
@解説@
(1)
Aは8時間、Bは3時間、Cは1時間で1周する。
24時間後、A・B・Cは同時に0に戻ってくるので、答えはすべて24時間以内になる。
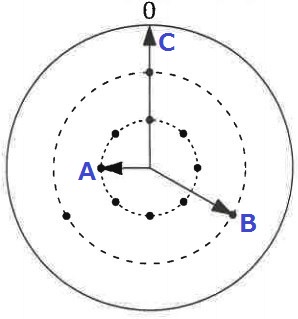
絞りやすいのはA。
Aが左を最初に指すのは〔8の倍数+6時〕だから、6時、14時、22時のいずれか。
Bが右下を指すのは〔3の倍数+1時〕なので、22時にしかない。
22時
(2)
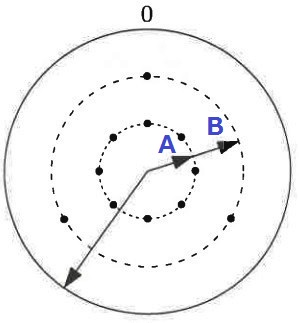
まずはAで絞る。
Aは〔8の倍数+1時〕⇒1時、9時、17時のいずれか。
Bは〔3の倍数時〕⇒9時台が確定。
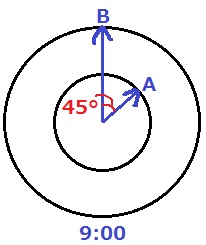
各々の1分あたりの角速度を求める。
A;360÷8÷60=3/4°
B;360÷3÷60=2°
1分あたり、2-3/4=5/4°ずつ近づいていく。
9時では45°離れているので、45÷5/4=36分後
9時36分
(3)

ここもAから絞る。
Aは〔8の倍数+3時〕→3時、11時、19時
Bは〔3の倍数+1時〕→19時台が確定。
1分あたりの角速度は、
A;3/4°
B;2°
C;360÷60=6°

↑19時の様子。
ここでシャドーを使う。AとCの真ん中にシャドーを設置。
シャドーの角速度はAとCの平均で、1分あたり(3/4+6)÷2=27/8°
このシャドーはAとCの真ん中を常に移動する。
シャドーとBが重なるとき、BはAとCの真ん中にある。
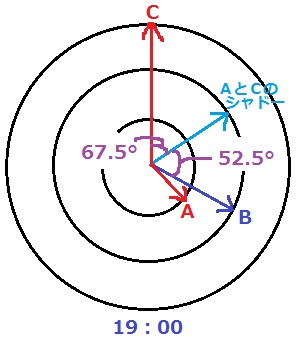
19時のとき、AC間は135°だから、シャドーとCは135÷2=67.5°
BC間は120°なので、シャドーとBは120-67.5=52.5°離れている。
シャドーはBに1分あたり、27/8-2=11/8°ずつ近づく。
52.5÷11/8=420/11分
答えは、19時420/11分(38・2/11分)



コメント