問題PDF
あるお店では、原価が1個3000円の品物を仕入れ、毎日定価を変えて売っています。
仕入れは毎日おこなっていて、日によって仕入れる個数が違いますが、
売れ残った品物は翌日以降に売ることはありません。このとき、次の問いに答えなさい。
(1) 正解率72.2%
ある日、品物をその日の定価で売り、仕入れた個数の1/5が売れ残りましたが、
損失がでませんでした。定価は最も安くて何円ですか。
(2) 正解率74.7%
次の日は品物を48個仕入れて2割の利益を見込んで定価をつけました。
そのうち何個かは定価で売れましたが、売れ残りそうだったので、
途中から定価の3割引きで売ったところ、この日の仕入れた個数は売れ残りました。
その結果、12600円の利益がありました。割引きをして売った個数は何個ですか。
なお、この問題は解答までの考え方を表す式や文章・図などを書きなさい。
(3) 正解率19.7%
さらに次の日は、定価を4500円にしました。
仕入れた個数の1/9が売れ残ると予想していましたが、
実際に売れ残った個数は予想の2/5だったため、利益は予想よりも27000円多くなりました。
この日に売った個数は何個ですか。
@解説@
2回目の合格者最低点は53点でした。
(1)
仕入れた個数を⑤とおくと、売れた個数は④、売れ残った個数は①
【売れた④×利益=残った①×原価】で損益分岐点となる。
原価は3000円なので、④×利益=①×3000
利益は3000÷4=750円
定価は3000+750=3750円にすればいい。
(2)
定価は3000×12/10=3600円(利益は600円)
割引後の売値は、3600×7/10=2520円(損失は480円)
鶴亀算。
仮にすべて利益600円で売れたとしたら、600×48=28800円の利益になる。
しかし、現実の利益は12600円だから、28800-12600=16200円の差。
利益+600を損失-480円に替えると、1個あたり1080円の差なので、
割引後の個数は16200÷180=15個
(3)
本試験で最も正解率の低かった問題。
分母の最小公倍数である【45】個仕入れたとする。
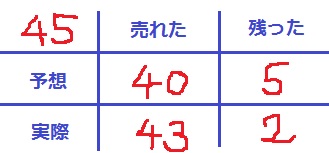
表で整理しよう。赤い数字は割合。
実際は【43】-【40】=【3】個多く売れたことになる。
注意すべき点は、仕入れの損失がなくなった分も利益に上乗せすること!
(売れ残りの仕入れ値は損失となるところ、その損失が回避されたことによる利益)
原価3000円、利益1500円。
予想よりも大きい利益となった27000円は、
【3】個売って得られる利益と【3】個の仕入れ値を合算したもの。
1500×【3】+3000×【3】
=4500×【3】=27000円
【1】=27000÷4500÷【3】=2個
実際に売れた【43】は、2×43=86個



コメント