問題ＰＤＦ
あるお店では、銅のメダル７枚は銀のメダル２枚に交換され、
銀のメダル７枚は金のメダル２枚に交換されます。
銅のメダルが７枚以上の場合は必ず銀のメダルに、
銀のメダルが７枚以上の場合は必ず金のメダルに交換します。
このとき、次の〔 〕に当てはまる数をそれぞれ答えなさい。
（１）
銅のメダル64枚を交換すると、金のメダル〔 ア 〕枚、
銀のメダル〔 イ 〕枚、銅のメダル〔 ウ 〕枚になります。
（２）
銅のメダル〔 エ 〕枚を交換すると、金のメダル４枚、銀のメダル６枚、
銅のメダル３枚になります。
（３）
Ａさんは、金のメダル２枚、銀のメダル５枚、銅のメダル３枚を持っています。
Ｂさんは、銀のメダルと銅のメダルだけを持っており、
銀のメダルと銅のメダルの枚数の比は１：２です。
ＡさんとＢさんの持っているメダルと合わせて、交換をしたところ、
金のメダル６枚、銀のメダル１枚、銅のメダル１枚になりました。
このとき、Ｂさんがはじめに持っていた銀のメダルは〔 オ 〕枚です。
＠解説＠
（１）
連比で銅と金の交換比率を確認。
〔銅49枚＝金４枚〕
①銅64枚のうち、銅49枚を金４枚に交換。
②残りの銅15枚で〔銅７枚＝銀２枚〕だから、銅14枚を銀４枚に交換。
よって、金４枚、銀４枚、銅１枚。
ア…４、イ…４、ウ…１
（２）
金４枚⇒銅49枚
銀６枚⇒銅：銀＝７：２なので、21枚
したがって、49＋21＋３＝73枚
エ…73
（３）
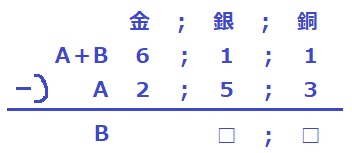
筆算で表すとこうなる。
（Ａ＋Ｂ）－Ａ＝Ｂ
Ｂは銀・銅のみ。金から銀へ繰り下げする。
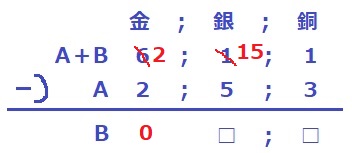
金４枚を銀14枚に繰り下げ。
すると、金は２枚となり、２－２＝０で金が消える。
以降、銀と銅しか考えない。
今度は銀から銅へ繰り下げ。
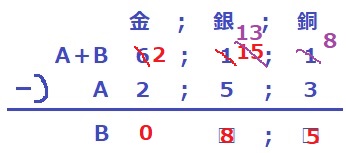
銀２枚を銅７枚に繰り下げ。
引き算すると、Ｂの銀は８枚、銅は５枚。
ここから銀と銅の枚数比を１：２にする。
銀２枚を銅７枚にチェンジすると、銀：銅＝６枚：12枚＝１：２
よって、Ｂの銀は６枚。
オ…６
難関中（算数科）解説ページに戻る
コメント