2018年度　東海中学過去問【算数】大問７解説

問題ＰＤＦ
Ａ町からＢ町まで行くバスは、途中Ｐ、Ｑ、Ｒの３つの地点に、この順にとまります。
あるバスがＡ町から10人を乗せて出発し、Ｐ地点では２人がバスを降りて５人が乗り、
Ｑ地点では４人が降りて３人が乗り、Ｒ地点では７人が降りて６人が乗り、
Ｂ町で全員降りました。ただし、運転手は人数にふくめません。
ＡからＱまでの２区間だけ乗った人数は、ＡからＰまでの１区間だけ乗った人数と、
ＰからＱまでの１区間だけ乗った人数の合計を同じでした。

（１）
Ｑで降りた人のうち、Ａから乗った人とＰから乗った人はそれぞれ何人ですか。

また、３区間だけ乗った人数と４区間乗った人数は同じで、
２区間だけ乗った人数の合計は、３区間だけ乗った人数の合計の２倍より１人多かった。

（２）
１区間だけ乗った人数の合計は何人ですか。

（３）
Ｂで降りた人のうち、Ａから乗った人とＰから乗った人はそれぞれ何人ですか。

＠解説＠
（１）
推論問題は情報整理がカギ。
はじめの検討対象はＡ－Ｐ－Ｑ間のみ。

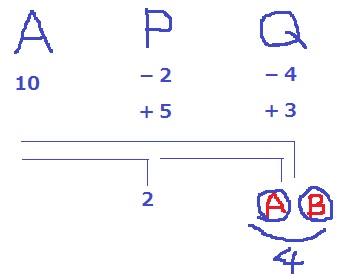
問題文から【Ａ－Ｑ間＝Ａ－Ｐ間＋Ｐ－Ｑ間】
Ｐで降りた２人はＡから必ず乗ったので、Ａ－Ｐ間は２人。
Ｐ－Ｑ間をＡ、Ａ－Ｑ間をＢとおく。
Ｑで降りるのは４人なので、Ａ＋Ｂ＝４
また、問題文からＢ＝Ａ＋２
Ｂ＞Ａで２つの等式が成り立つ組み合わせは、Ａ＝１、Ｂ＝３しかない。
Ａから乗った人…３人、Ｐから乗った人…１人

（２）（３）

全部のパターンを図示。
青い数字が乗ってくる人数。赤い数字が降りる人数。
（青い数字は横の合計、うえの赤い数字は縦の合計）

Ｒで乗る６人は必ずＢで降りるので、右下は６。
問題文より、【３区間だけの人＝４区間だけの人】
４区間はＡ－Ｂ間（Ｂ）、３区間はＡ－Ｒ間（Ａ）とＰ－Ｂ間（Ｃ）
【Ｂ＝Ａ＋Ｃ】
・１行目から、Ａ＋Ｂの和は10－２－３＝５
・２行目から、Ｃは５－１＝４以下
・一番左の列から、Ｂ＋Ｃの和は11－６＝５以下

最初のＡ＋Ｂ＝５から、【Ｂ＝Ａ＋Ｃ】を組み合わせを考える。
Ｂ＝Ａ＋Ｃ
５＝０＋５　…Ｃが４以下ではない不適
４＝１＋３　…Ｂ＋Ｃの和が５以下ではない。
３＝２＋１
Ｂが２以下だとＡがＢより大きくなり、等式が成り立たない。
【Ａ…２、Ｂ…３、Ｃ…１】

２区間のＤ・Ｅを追加。引き算だけで残りもすぐ埋まる。
Ｄ＝５－１－１＝３
Ｅ＝11－３－１－６＝１
Ｄの下＝７－２－３＝２

一応確認してみると、３区間だけ…２＋１＝３人、２区間だけ…３＋３＋１＝７人
３×２＋１＝７と条件に適合する。
（２）１区間だけ乗った人数の合計･･11人
（３）Ａから３人、Ｐから１人、Ｑから１人
難関中（算数科）解説ページに戻る