2022年度　甲陽学院中学１日目過去問【算数】大問６解説

問題ＰＤＦ
図のような三角形を、直線ＡＢを軸として回転させます。

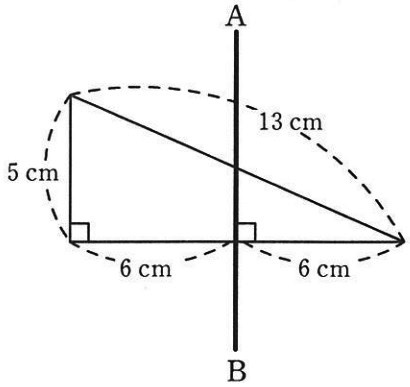
（１）
１回転させてできる立体の体積を求めなさい。
ただし、円すいの体積は（底面積）×（高さ）÷３で求められます。

（２）
90度回転させてできる立体の表面積を求めなさい。

＠解説＠
（１）

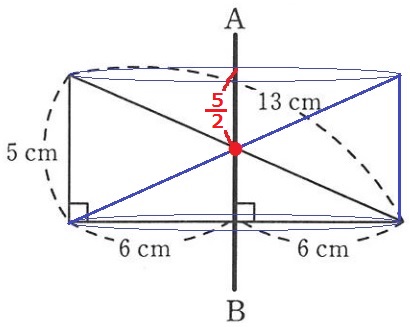
高さ５ｃｍの円柱から、上半分の円錐をひけばいい。
６×６×3.14×５－６×６×3.14×５/２÷３
＝180×3.14－30×3.14
＝（180－30）×3.14＝471ｃｍ³

（２）

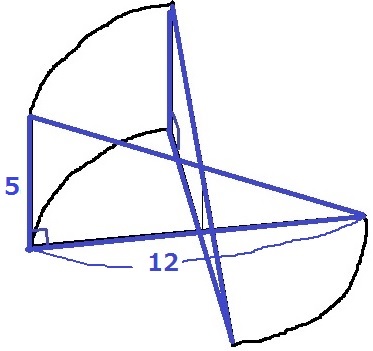
↑歪みましたが、このような回転体になる。
２つの三角形が表面に露出している。

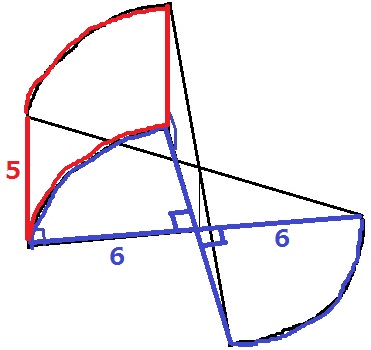
底面は半径６ｃｍの４分の１円が２つ。赤い側面積も出しやすい。

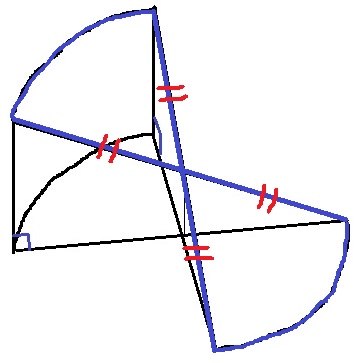
大問題はコチラ(;`ω´)
ナナメに傾いているので、直径13ｃｍの円ではない。

交点が真ん中であることから、柱体の２階部分を錐で区切り、
これをひっくり返して１階へ下ろしてみる。
すると、ナナメの部分は底面の半径が６ｃｍ、母線が13/２ｃｍの円錐の半分になる。
【円錐の側面積＝母線×半径×3.14】
したがって、12×５÷２×２＋６×６×3.14×１/２＋６×２×3.14×１/４×５＋13/２×６×3.14×１/２
＝60＋（18＋15＋19.5）×3.14
＝60＋52.5×3.14
＝60＋164.85
＝224.85ｃｍ²

＠円錐の側面積＠

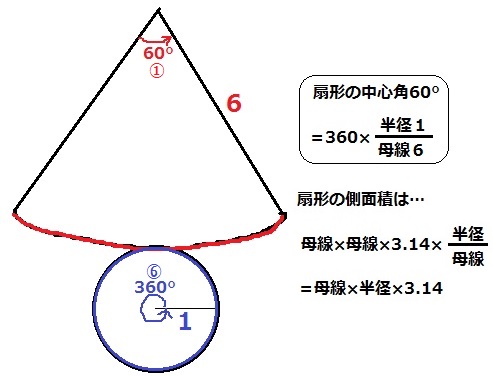
底面の円周（青）と側面の扇形の弧（赤）の長さが等しい。
半径１、母線６とすると、
【１×２×3.14＝６×２×3.14×１/６】で等式になる。
扇形の中心角は、360×１/６＝60°
中心角の比は、円：扇形＝360：60＝⑥：①で半径と母線の逆比にあたる。
扇形の中心角は〔×半径/母線〕に置き換えることができる。
円錐の側面積は、母線×母線×3.14×半径/母線＝母線×半径×3.14
難関中（算数科）解説ページに戻る