問題ＰＤＦ
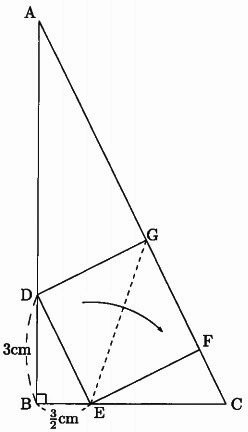
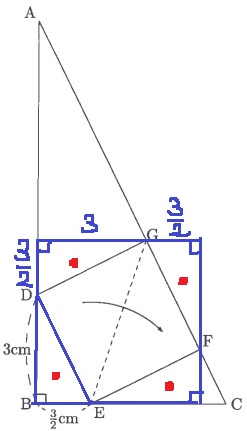
図の三角形ＡＢＣは直角三角形で、四角形ＤＥＦＧは正方形です。
次の問いに答えなさい。
（１）
四角形ＤＥＦＧの面積は何ｃｍ2ですか。
（２）
対角線ＥＧを折り目として、三角形ＡＢＣを折りました。
折られた図形について、
①重なっている部分の周を解答らんのマス目にあわせて正確に太線でかき入れなさい。
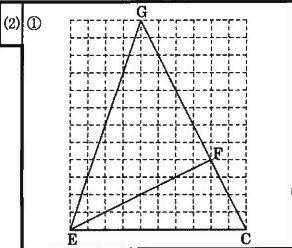
②重なっていない部分の面積は、あわせて何ｃｍ2ですか。
＠解説＠
（１）
ヒントが少ないので角度を調査。
●＋×＝90°を手掛かりに等角を記していくと、
相似図形がたくさんあらわれる。
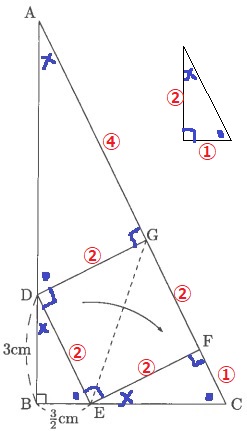
最も短い辺ＦＣを①とする。
ＥＦ＝②、正方形の１辺は②。
ＤＧ＝②から、ＡＧ＝④
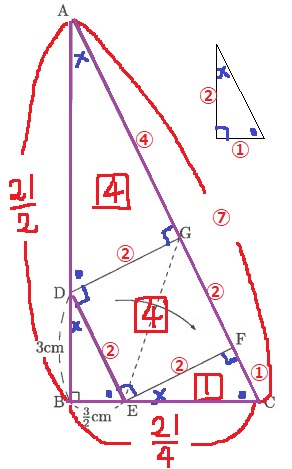
△ＡＢＣ∽△ＤＢＥ
辺の比は、ＡＣ：ＤＥ＝⑦：②
ＡＢ＝３×７/２＝21/２ｃｍ
ＢＣ＝21/２÷２＝21/４ｃｍ
△ＡＢＣと△ＤＢＥの面積比は、⑦2：②2＝49：４
△ＡＢＣの面積を49とすると、四角形ＡＤＥＣの面積は45となる。
△ＡＤＧの面積…④×②÷２＝【４】
正方形ＤＥＦＧ…②×②＝【４】
△ＥＣＦ＝②×①÷２＝【１】
正方形ＤＥＦＧの面積は、
21/４×21/２×１/２×45/49×４/９＝45/４ｃｍ2
＠別解＠
３＋３/２＝９/２
９/２×９/２－３×３/２×１/２×４＝45/４ｃｍ2
（２）①
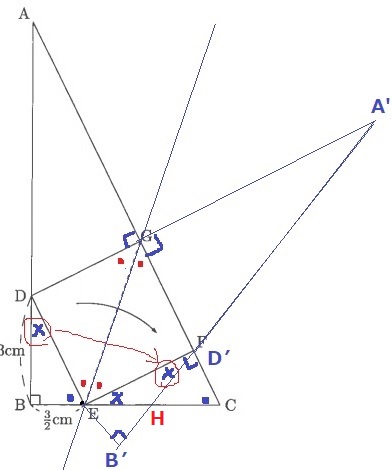
直線と直角を意識して、右側へ対称移動。
ＤはＦと重なる。
ＢＣとＡ’Ｂ’の交点をＨとして、∠ＢＤＥ＝×を∠Ｂ’Ｄ’Ｅに移動させると、
２つの底角が等しくなり、△ＥＦＨはＨＥ＝ＨＦとする二等辺三角形。
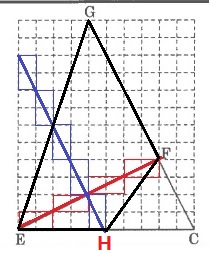
ＨはＥＦの垂直二等分線上にある。
（すなわち、ＥＦの中点を通る垂線）
ＥＦ（赤線）が右２上１なので、青線は右１下２で垂直となる。
青線とＥＣとの交点がＨとなり、重なっている部分を太線で描く。
②
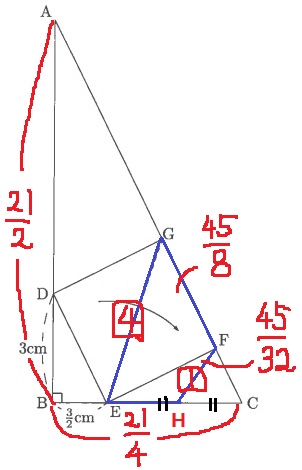
全体（△ＡＢＣ）－重なっている四角形ＧＥＨＦ×２＝重なっていない部分
（１）より、正方形ＤＥＦＧは45/４ｃｍ2だから、
△ＥＦＧ＝45/４÷２＝45/８ｃｍ2
正方形ＤＥＦＧの面積を【４】とおくと、△ＥＦＣは【１】であった。
（２）①の解答欄でＨはＥＣの中点にある。
△ＥＦＨ＝45/４×１/４×１/２＝45/32ｃｍ2
よって、21/４×21/２×１/２－（45/８＋45/32）×２
＝441/16－225/16＝216/16＝27/２ｃｍ2
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント