2021年度　早稲田実業学校中等部過去問【算数】大問５解説

問題ＰＤＦ
紙の折り方には山折りと谷折りがあり、それぞれ図１のような折り方をします。
いま、縦9ｃｍ、横12ｃｍの長方形の方眼紙ＡＢＣＤがあります。次の各問いに答えなさい。

（１）
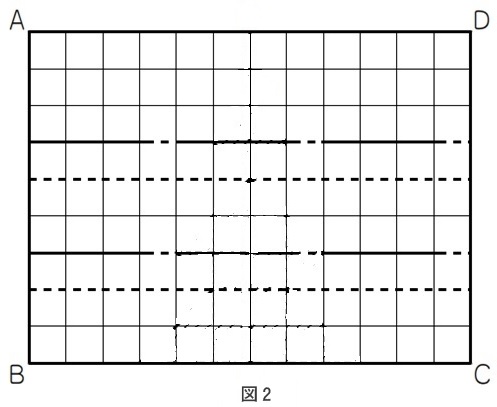
図２のように紙を折ったとき、縦の長さは何ｃｍになりますか。

（２）
図２のあと、図３のように紙を折りました。
ＢＦ上に点Ｑをとり、ＰＱに沿って三角形ＰＦＱを切り取って広げた図形を、図形アとします。
次の①、②に答えなさい。
①ＦＱの長さが３ｃｍのとき、図形アとして切り取られた部分を解答用紙の図にかき、斜線で示しなさい。

②図形アの面積が20ｃｍ²のとき、ＦＱの長さを求めなさい。

＠解説＠
（１）

４行なくなる。５ｃｍ

（２）①

青で囲んだ４行がなくなる。
折ったあとにＰと重なる点をＰ’とする。
Ｐ’Ｆ＝３ｃｍ
切り取った直角二等辺三角形Ｐ’ＦＱだけを図示すると、うえのようになる。

ＥＦの折り目を戻すと左右で線対称。

最後に横の折り目で線対称。１ｃｍごとに上へ２連続、対称移動する。
実際の解答は斜線で描くこと。

②

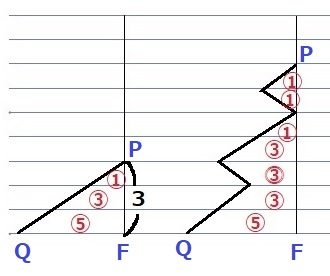
切り取った直角三角形ＰＦＱの面積比を高さ１ｃｍごとに分けると、
面積比はそれぞれ①：③：⑤。
紙を広げると、右図のようになる。

図形アの半分である10ｃｍ²が⑰にあたる。
直角三角形ＰＦＱの面積は、10×⑨/⑰＝90/17ｃｍ²
ＦＱの長さは、90/17×２÷３＝60/17ｃｍ
難関中（算数科）解説ページに戻る