問題ＰＤＦ
図のような直方体があり、辺ＡＢ上に点Ｐを、辺ＢＣ上に点Ｑを、ＰＢとＱＢの長さがどちらも２ｃｍになるようにとります。また、辺ＥＦ上に点Ｒを、辺ＦＧ上に点Ｓを、ＲＦとＳＦの長さがどちらも６ｃｍになるようにとります。４点Ｐ、Ｑ、Ｒ、Ｓを通る平面でこの直方体を切り、点Ａを含むほうの立体を（あ）とします。
このとき、次の各問いに答えなさい。
ただし、角すいの体積は、（底面積）×（高さ）÷３で求められるものとします。
（１）
立体（あ）の体積は何ｃｍ3ですか。
（２）
立体（あ）を面ＰＱＲＳが底面になるように平らなゆかの上におきます。
このとき、点Ｄはゆかから何ｃｍの高さにありますか。
＠解説＠
（１）
ＲＰ、ＣＱ、ＦＢを延長した交点をＯとする。
三角錐Ｏ－ＰＢＱと三角錐Ｏ－ＲＦＳの相似比は１：３。
→体積比は相似比の３乗で１：27。
Ａを含まない立体（角錐台ＰＢＱ―ＲＦＳ）は、
６×６÷２×12÷３×26/27＝208/３ｃｍ3
直方体からこれを除いて、（あ）の体積を求める。
10×12×８－208/３=2672/３ｃｍ3
（２）
難問です:;(∩´＿`∩);:
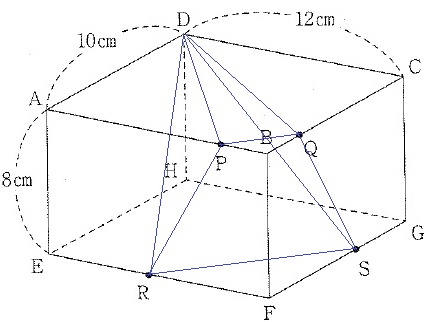
断面ＰＲＳＱを底面としたときの四角錘ＤーＰＲＳＱの高さを求める。
（１）の三角錐Ｏ－ＰＢＱは、底辺の三角形の１辺と錘の高さが１：２であった。
ここから例の展開図を作成。
三角錐Ｏ－ＰＢＱを展開すると正方形になる。
（知識問題ですが、中学受験の算数では必ず授業で習う有名錐なので使えるようにしておこう！）
正方形から周りの３つの三角形をひくと、△ＯＰＱは６ｃｍ2となる。
このあとが手詰まる。。
ここで、四角形ＰＲＳＱと△ＯＰＱは同一平面にあることに注目する。
面ＰＲＳＱが底面になる場合＝面ＯＰＱが底面になる場合。
ということは、四角錘Ｄ―ＰＲＳＱの高さは三角錐Ｄ―ＯＰＱと同じである！
ＤＯを結んでみよう。
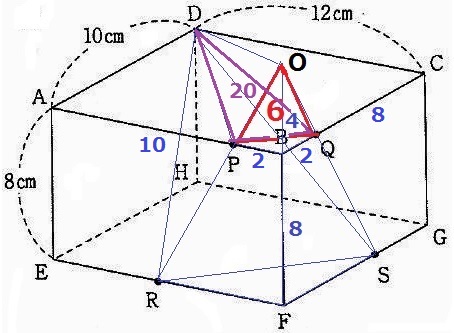
△ＤＰＱの面積は、長方形ＡＢＣＤ内で周りの３つの三角形をひく。
△ＤＰＱ＝10×12－10×10÷２ー12×８÷２－２＝20ｃｍ2
三角錐Ｏ－ＤＰＱの体積は、20×４÷３＝80/３ｃｍ3
三角錐Ｏ－ＤＰＱの高さは、80/３×３÷６＝40/３ｃｍ
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント