2019年度　高槻中学過去問Ａ日程【算数】大問４解説

問題ＰＤＦ
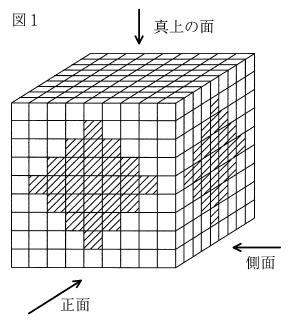
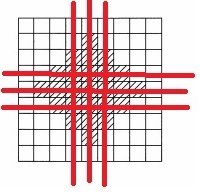
図１のように小さな立方体を縦、横ともに９個ずつ９段積み上げて、
大きな立方体を作りました。

（１）
この立方体から図２の斜線部の位置にある小さな立方体を
正面から反対の面までつらぬいてぬき取りしました。
ぬき取った小さな立方体は合計何個ですか。
ただし、この大きな立方体は小さな立方体をぬき取ってもくずれないものとします。

（２）
（１）から、さらに、側面からも図２の斜線部の位置にある小さな立方体を
同じようにぬき取りました。２つの方向からぬき取った小さな立方体は合計何個ですか。

（３）

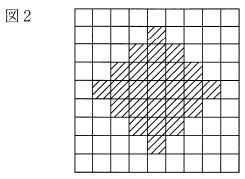
（２）から、さらに、真上の面からも図２の斜線部の位置にある小さな立方体を
同じようにぬき取りました。３つの方向からぬき取った小さな立方体は合計何個ですか。

＠解説＠
本番を向かえるために、類題は解いておきたいところです。
（１）
正面から抜く。
１＋３＋５＋７＋５＋３＋１
＝９＋７＋９＝25
奥行きが９個なので、
25×９＝225個

（２）
側面からも抜く。
側面のみだと前問と同じく、225個の立方体がぬかれる。
225＋225＝450個

ここから、ダブったところを引く。
ダブった立体は正八面体のような形になる。

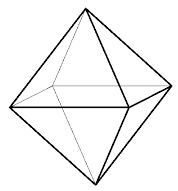
２段目は１×１、３段目は３×３、４段目は５×５、５段目は７×７、
６段目は５×５、７段目は３×３、８段目は１×１
１＋９＋25＋49＋25＋９＋１
＝35＋49＋35＝119個

したがって、450－119＝331個

（３）
真上からも切り抜く。
１段ずつ判定していく。

１段目と９段目はどこもダブらないので、25個×２＝50個

２段目と８段目は十字の部分がすでになくなっている。

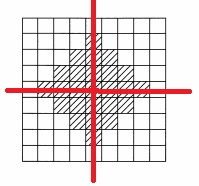
残りは12個。12×２＝24個

３段目と７段目は３列ずつかぶるが、
すると、どこも新しくぬき取られないことになる。
４・５・６段目も同じくぬき取られない。

よって、新しくぬき取られるのは、50＋24＝74個
331＋74＝405個
難関中（算数科）解説ページに戻る

◆menu◆ 公立高校入試…関東圏メイン。千葉だけ５教科あります。％は正答率。
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→