2023年度　京華中学１回目午後過去問【算数】大問３解説

問題ＰＤＦ
（１）
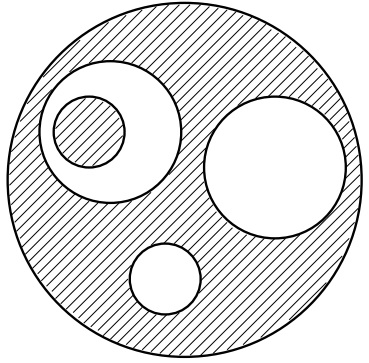
次の図のように、半径10ｃｍの円の中に、半径４ｃｍの円と半径２ｃｍの円を２個ずつかきました。
斜線部分の面積の和は何ｃｍ²ですか。

（２）
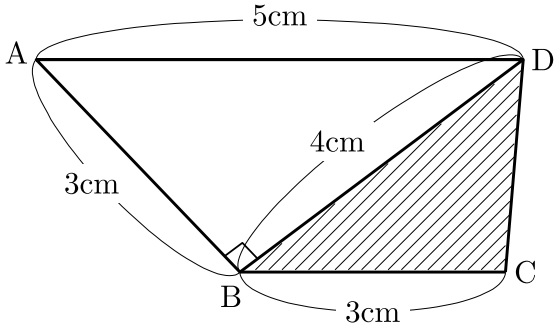
次の図で、四角形ＡＢＣＤは台形です。斜線部分の面積は何ｃｍ²ですか。

（３）
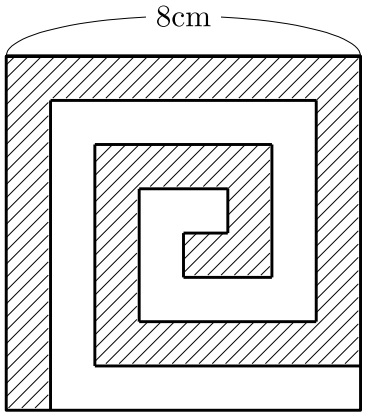
次の図のように、１辺８ｃｍの正方形を１ｃｍの幅でうず巻き状に分けました。
斜線部分と残りの部分の周りの長さの差は何ｃｍですか。

（４）
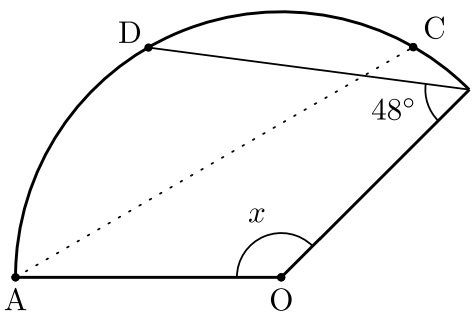
次の図で、おうぎ形を直線ＡＣで折ると、Ｏはおうぎ形の周上の点Ｄに重なります。
ｘの角の大きさは何度ですか。

＠解説＠
（１）

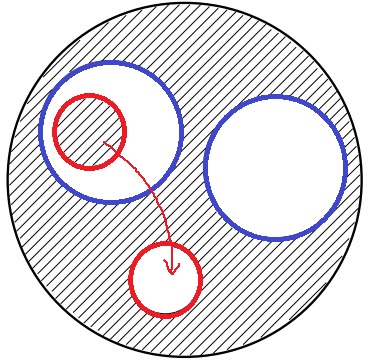
半径２ｃｍ（赤い円）を移動して埋める。
半径10ｃｍの円から２つの半径４ｃｍの円（青い円）を引けばいい。
10×10×3.14－４×４×3.14×２
＝（100－32）×3.14
＝213.52ｃｍ²

（２）

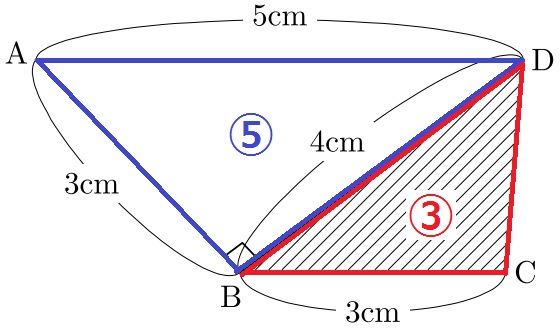
△ＡＢＤの面積は、３×４÷２＝６ｃｍ²
四角形ＡＢＣＤは台形なので、
△ＡＢＤ：△ＢＣＤ＝ＡＤ（上底）：ＢＣ（下底）＝⑤：③
△ＢＣＤ＝６×③/⑤＝18/５ｃｍ²

（３）

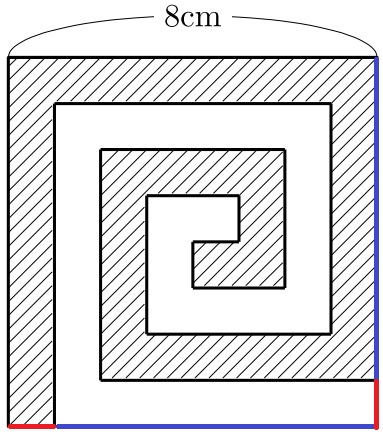
求めたいのは周りの長さの差。
斜線と白地が接している部分は共通だから除外。
差が出るのは外側。青線と赤線が同じ長さなので、斜線部分の方が８＋８＝16ｃｍ長い。
16ｃｍ

（４）

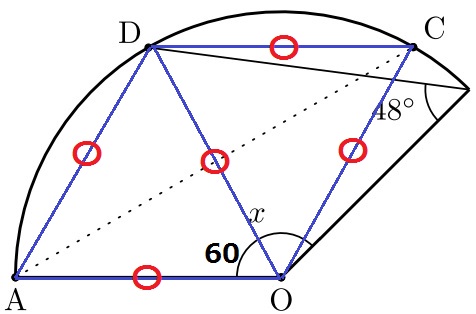
折り返し→線対称
半径から、ＡＯ＝ＤＯ＝ＣＯ
線対称から、ＡＤ＝ＡＯ、ＣＤ＝ＣＯ
これら５辺の長さは等しい。
△ＡＯＤは正三角形→∠ＡＯＤ＝60°

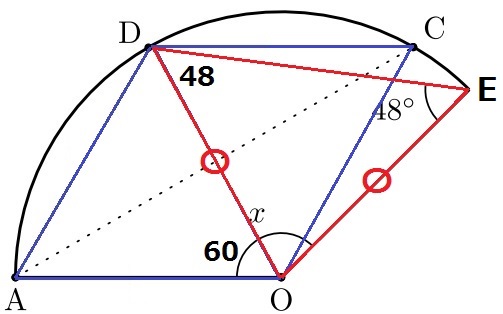
右端の点をＥとする。△ＤＯＥは二等辺三角形。
∠ＤＯＥ＝180－48×２＝84°
ｘ＝60＋84＝144°
難関中（算数科）解説ページに戻る