問題ＰＤＦ
図のように、平らな広い台の上に、三角すいＡＢＣＤが置いてあります。
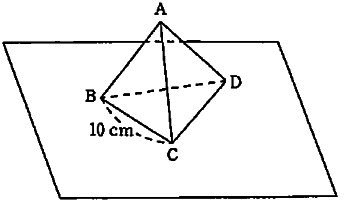
この三角すいの４つの面はすべて１辺10ｃｍの正三角形です。
１匹の小さいアリがこの三角すいの頂点Ａから出発して、毎秒１ｃｍの速さで三角すいの面や台の上を進みます。
ただし、アリの大きさは考えません。また、アリが三角すいと台の間に入ることはありません。
（１）
アリがＡを出発してから10秒以内に進める範囲の面積を求めなさい。
（２）
アリがＡを出発してから15秒以内に進める範囲の面積を求めなさい。
＠解説＠
（１）
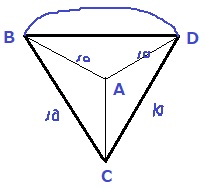
ＡからＢＤ方向に10ｃｍ進んだ様子を上から見るとこんな感じになる。
Ａ－ＢＣＤは立体（正四角錐）であることに注意！
ＡからＢ、Ｄまではちょうど10ｃｍ。
正四角錐より先は台の上で扇形に広がる。
平面図（上から見た図）に引き直せば、∠ＢＣＤを中心角とした扇形と同じ。
（立体では、∠ＢＡＤを中心角とする）
ＢＣ方向とＣＤ方向を含めると、中心角60°の扇形が３つ。
10×10×3.14×60/360×３＝157ｃｍ2
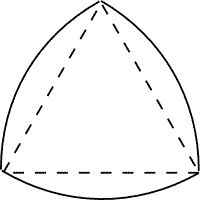
上から見ると、ルーローの三角形になる。
（２）
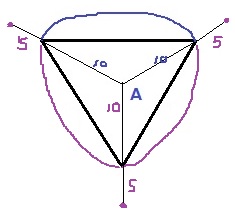
15ｃｍ動くので、直線部分はここまでいく。
弧の部分も平行して５ｃｍ外側を周る。
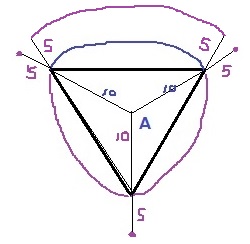
（１）と同様に平面で考えると、中心角60°、半径15ｃｍの扇形となる。
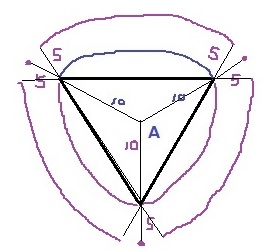
３方向に描写。
留意すべき点は、あいだの部分は別の扇形になる。
三角錐の頂点から５ｃｍの扇形。
中心角は、底面の正三角形の内角から対頂角を利用して60°
15×15×3.14×60/360×３＋５×５×3.14×60/360×３
＝（15×15＋５×５）×3.14×１/２
＝250×3.14×１/２
＝125×3.14＝392.5ｃｍ2
平面で形を捉え、立体に戻して扇形を３つ数えるのがミソ。
難関中（算数科）解説ページに戻る
コメント