問題PDF
流れの速さが毎分36mの川の下流にア町、上流にイ町があります。この区間を2そうの船A、Bが往復しています。Aが上流に向かって進む速さとBが下流に向かって進む速さは同じです。
この2そうの船A、Bが、ア町からイ町に向かって同時に出発しました。Aがイ町に到着したとき、Bはイ町より1728m下流の地点にいました。その後Aはすぐにア町に向かって戻り、途中Bとすれ違った後、出発してから40分後にア町に戻りました。
下のグラフは、2そうの船がア町を出発してからの時間と、ア町からの距離を表したものです。
ただし、清水時での船の速さはそれぞれ一定であるとします。

(1)
静水時での船A、Bの速さの差は、毎分何mですか。
(2)
静水時での船Aの速さは毎分何mですか。
(3)
船A、Bが2度目にすれ違ったのは、ア町から何m上流の地点ですか。
@解説@
(1)
グラフばかりに目がいくと、初問でつまづいて全敗する(;´・ω・)
差の1728mは使わない。
用いるのは『Aの上流とBの下流の速さが同じ』
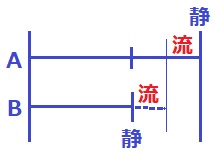
上流の速さ=静水時の速さ-流れの速さ
下流の速さ=静水時の速さ+流れの速さ
Aの上流とBの下流の速さが等しいということは、
静水時のAとBの差は流れ2つ分。
36×2=毎分72m
(2)

静水時のAとBの速さの差が毎分72m➡流れの速さを引いた上流の速さの差も72m。
AとBが同時に出発して1728mの差がでたということは、1728÷72=24分
Aの上りは24分で、Aの下りは40-24=16分
時間の比は、上り:下り=24:16=3:2
速さは逆比で、上り:下り=②:③
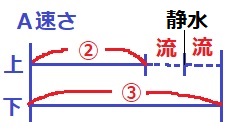
①…流れの2倍で毎分72m。
Aの静水時の速さは、72×②+36=毎分180m
(3)
Aの上りは、180-36=毎分144m
(1)より、AとBの速さの差は毎分72m(上りの差も同様)
Bの上りは144-72=毎分72m
上りの速さが、A:B=144:72=2:1

時間は逆比で1:2だから、Bがイ町に着くのは24×2=48分
Aの上りとBの下りは時間が等しいので、Bがア町に戻るのは48+24=72分
赤い三角形に注目!
速さが同じ→傾きの角度が一緒で底角が等しく二等辺三角形。
AとBが2度目にすれ違う時間は、40と72の真ん中である56分。
すなわち、Aがふたたびア町を出発してから16分後である。
144×16=2304m



コメント