問題PDF
(1)
次の問いに答えなさい。
(あ)2023を2回かけあわせたものを23で割った余りを求めなさい。
(い)2023を2023回かけあわせたものを23で割った余りを求めなさい。
(2)
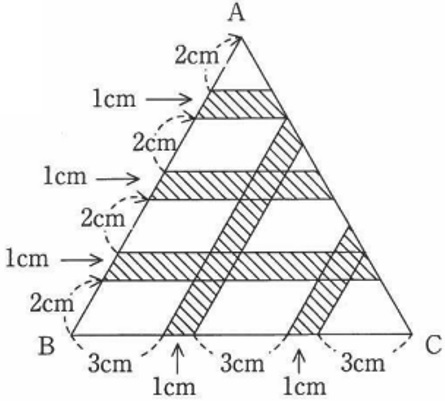
三角形ABCの面積と斜線部分の面積の比を最も簡単な整数の比で答えなさい。
ただし、三角形ABCの中にある線はすべて辺AB、BCと平行とします。
(3)
次の〔 〕に当てはまる整数を2組答えなさい。

ただし、〔 う 〕<〔 え 〕<〔 お 〕<〔 か 〕であり、
〔 〕には2けたの整数が入ってもよい。
@解説@
(1)あ
年度問題。
2023÷23=87…22
余りが22ということは、2023+1=2024は23の倍数。
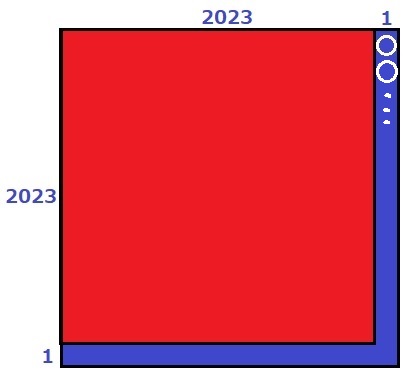
2024が23の倍数だから、2024×2024も23の倍数。
2024×2024÷23の余りは0。
1辺2024の正方形から青い領域を除外する。
1個の〇を除外すると、余り0から1つ減るので余り22、
2個の〇を除外すると、余り0から2つ減るので余り21になる。
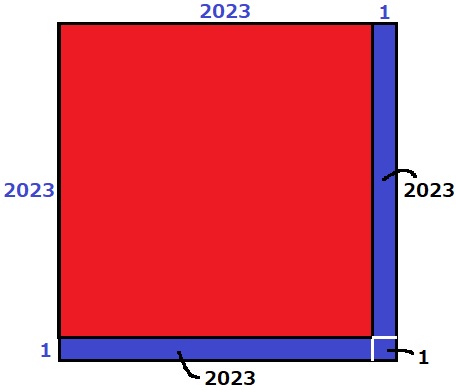
2023÷23の余りが22だったから、青い領域は余り22+余り22+余り1=余り45
45÷23=1…22→余り22
余り0(余り23)から22を除外して余り1
い

2023を3回かけた数(2023×2023×2023)は、1辺2023の正方形が2023個ある。
おのおのの正方形を23で割った余りは1だから、この数を23で割った余りは2023である。
つまり、2023を3回かけた数の余りは2023を1回かけた数の余りと同じ22!
整理すると、2023×2023⇒2023(余り22)を2023回かけて余り1。
2023×2023×2023⇒2023×2023(余り1)を2023回かけて余り22。
2023×2023×2023×2023⇒2023×2023×2023(余り22)を2023回かけて余り1…。
2023を奇数回かけると余り22で、偶数回かけると余り1である。
2023を2023回かけた数の余りは22
(2)
必答問題。

隅に寄せる。
△ABCの面積比は、11×11=121
寄せた部分は、8×9=72
斜線部分は、121-72=49
△ABC:斜線=121:49
(3)
分子が1の単位分数。

〔う=え=お=か〕の場合は、1=1/4+1/4+1/4+1/4
〔う>え>お>か〕なので、1/〔う〕は1/4よりも大きい数でなくてはならない。
→〔う〕は2か3。
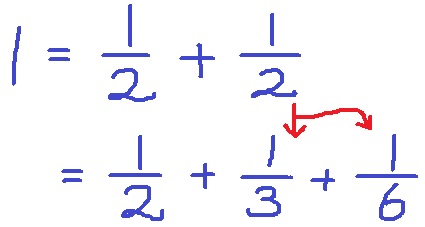
〔う〕=2とする。
1/2の次に大きい単位分数である1/3で1/2を分解してみる。
1/2-1/3=1/6

同じ要領で1/6を次に大きい1/7で分解する。
1=1/2+1/3+1/7+1/42
*ある単位分数は1個下の単位分数を使って必ず分解できる。
1/6-1/7=1/42→1/6=1/7+1/42
1/7-1/8=1/56→1/7=1/8+1/56
1/8-1/9=1/72→1/8=1/9+1/72
もう1組が厄介(´~`)

試しに〔う〕=3を入れてみると、うまくいかない。
3つ目までの和で分子が分母の75%を超えないといけないが、頑張って探しても無い…。
〔う〕=2しかないのでは?
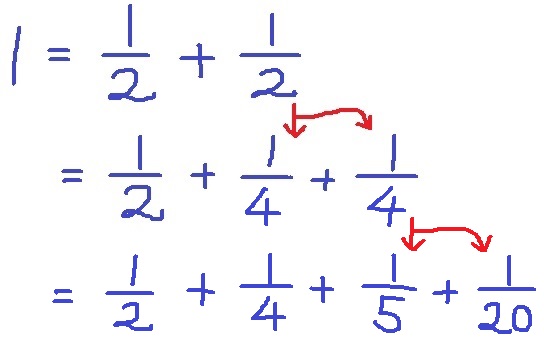
先ほどの1/3+1/6を1/4+1/4に変えて、1/4を分解すると成り立つ。
例:(う、え、お、か)=(2、3、7、42)(2、4、5、20)



コメント