問題PDF
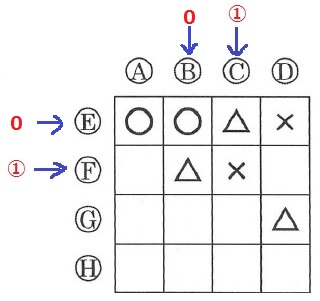
図1のような、16枚のパネルと8つのボタンA、B、C、D、E、F、G、Hがあります。
最初は、すべてのパネルに「〇」が表示されています。

ボタンA、B、C、Dはそれぞれのボタンの下に並ぶ縦4枚のパネルに対応し、ボタンE、F、G、Hはそれぞれのボタンの右に並ぶ横4枚のパネルに対応しています。各パネルは、対応するボタンが押されるたびに、〇→△→×→〇→△→×→〇→…と、表示されている記号が変化していきます。例えば、最初の状態から、ボタンAを押すと図2にようになり、さらにボタンE、ボタンAの順番で押すと、図3、4のように変化します。

(1)
最初の状態から、ボタンを次のような順番で押すと、どのようになりますか。
パネルに表示される記号を解答用紙の図に書き入れなさい。
①Aを1回、Bを1回、Cを2回、Eを2回、Fを2回、Hを1回
②Aを3回、Cを2回、Dを5回、Eを2回、Gを3回、Hを4回

(2)
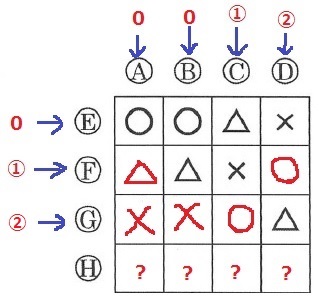
最初の状態から何回かボタンを押したところ、一番上の4枚のパネルに表示されている記号は、図5のようになりました。このとき、ボタンA、B、C、Dはそれぞれ何回押しましたか。以下の答え方にならって、考えられる組み合わせをすべて答えなさい。ただし、それぞれのボタンを押した回数は、最大で2回とします。
【答え方】()の中に、A、B、C、Dの順に押した回数を記入する。
例えば、Aを1回、Cを2回押し、B、Dを押さなかった場合、(1、0、2、0)と書く。

(3)
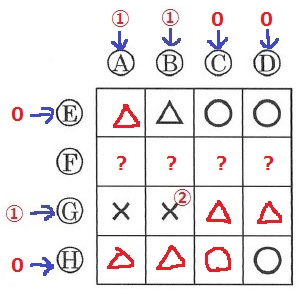
最初の状態から何回かボタンを押したところ、いくつかのパネルに表示されている記号は次の図のようになりました。記号のかかれていないパネルのうち、記号が1つに決まるパネルにはその記号を、決まらないパネルには「?」をかき入れなさい。

(4)
最初の状態から、ボタンA、Bは1回も押さず、ボタンCは1回、ボタンDは2回押しました。EからHのボタンはどのように押したか分からないとき、〇が表示されているパネルの枚数として考えられるものをすべて答えなさい。
(5)
最初の状態から何回かボタンを押したとき、〇が表示されているパネルの枚数として考えられるものをすべて答えなさい。
@解説@
(1)

押されたボタンの回数を調査。
②AとGの3回押しは押さないのと同義。
Dの5回は2回押し、Hの4回は1回押しでカウント。
(2)

E列のパネルなので、E列が何回押されたかで場合分け。
Eを先に押したあとでA~Dを考えたほうがやりやすい。
◆E0回押し→全部〇→(0、0、1、2)
◆E1回押し→全部△→(2、2、0、1)
◆E2回押し→全部×→(1、1、2、0)
(0、0、1、2)(2、2、0、1)(1、1、2、0)
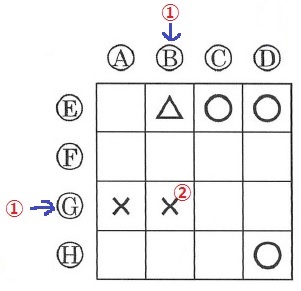
(3)①
ボタンが押された回数はわからないが、
3の倍数or3の倍数+1or3の倍数+2がわかればいい。
(以下、3の倍数…0、3の倍数+1…①、3の倍数+2…②と表記)

〔C・F〕の×に注目する。
×は②で、これをCとFで分配する。
上と左が△だから、Cは①、Fは①
〔B・F〕の△はFの①で変わったので、Bは0。
Eも0にしないと〔B・E〕が〇にならないから、Eも0。
Eが0だから、〔D・E〕を×にするにはDが②
〔D・G〕を△にするには、Gを②にする。
Hは決まらない。以上を整理すると上図になる。
②
〔B・G〕の×に注目。×の②をBとGに配分。
上の△からBは①、Gは①
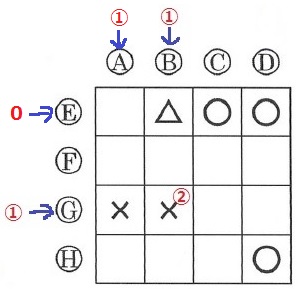
〔A・G〕を×にするためにAは①
〔B・E〕を△のままにするのにEは0。
〔C・E〕と〔D・E〕の〇からCとDは0。
〔D・H〕の〇からHも0。
Fは決まらない。以上を整理すると上図になる。
(4)

A~Dを指定回数分押した様子から考える。
E~Hをすべて押さないと〇は8個。
Eを1回押すと△△×〇、2回押すと××〇△
ボタンを押すと〇の数が1個減る。
E~Hの4列のうち、ボタンを押して〇を減らすと、
〇の数の組み合わせは4、5、6、7、8枚
(5)
調べ上げなので時間がかかる(;´Д`)
前問の解答より、縦のボタンで〇〇△×に固定して横を操作すると4~8枚であった。
そこで、縦のボタンをあらかじめ押してから横を考える。
以下、同じ数字の組み合わせは削除。
◆1種類
〇〇〇〇→(0・4)
◆2種類
〇〇〇△→(0・1・3)
〇〇△△→(0・2)
〇△△△→(0・1・3)
◆3種類
〇△××→(1・2)
〇△△×→(1・2)
〇〇△×→(1・2)
例えば、縦を押してすべての行を〇〇〇△にすると、
〇〇〇△
〇〇〇△
〇〇〇△
〇〇〇△
横のボタンをおすと、行に現れる〇の数は(0・1・3)だから、
0+0+0+0=0
0+0+0+1=1
0+0+1+1=2
0+1+1+1=3
0+3+3+3=9
1+3+3+3=10…が新たに作れる。
縦を押してすべての行を〇〇〇〇にすると、
0+4+4+4=12
4+4+4+4=16…が新たに作れる。
しかし、残りの〔11・13・14・15〕は作れない。
◆再掲◆
〇〇〇〇→0・4
〇〇〇△→0・1・3
〇〇△△→0・2
〇△××→1・2
11=4+4+3+0=4+4+2+1=4+3+3+1=4+3+2+2=3+3+3+2
(0・3・4)(1・2・4)(1・3・4)(2・3・4)(2・3)の組み合わせはない。
同様に、13=4+4+4+1=4+4+3+2=4+3+3+3
(1・4)(2・3・4)(3・4)の組み合わせはない。
15=4+4+4+3
(3・4)の組み合わせはない。
答えは、0、1、2、3、4、5、6、7、8、9、10、12、16枚。



コメント