問題ＰＤＦ
図のように、半径３ｃｍで中心角が90°のおうぎ形と、
１辺の長さが３ｃｍのひし形を組み合わせた図形を底面とする、高さが６ｃｍの立体があります。
点Ｐは、１→２→３→４→５→６→７→８→９→１の順で線に沿って動きます。点Ｐが６ｃｍの辺上を動くときの速さは、３ｃｍの辺上を動くときの速さの２倍です。上のグラフは、点Ｐが進んだ時間（秒）と道のり（ｃｍ）の関係を表したものです。グラフのア、イ、ウの空欄にあてはまる数を入れなさい。
＠解説＠
グラフの意味を確認。
Ｐは１から順番に動き、１に戻ってくる。
グラフの原点がスタートの１で、最後がゴールの１。あいだは２～９。
グラフが急なところは６ｃｍ、緩やかなところは３ｃｍ。
Ｐが６ｃｍの辺上を動くときは３ｃｍの辺上を動くときの速さの２倍なので、
６ｃｍと３ｃｍの辺上を動く時間は同じだから、横軸は等間隔になる。
ウから攻める。
ウは１～４までにＰが動いた距離。
６＋３＋３×２×3.14×１/４
＝９＋4.71＝13.71ｃｍ（ウ）
イが中途半端な場所なので、先にアを処理する。
アは１周したＰが動いた距離の合計。
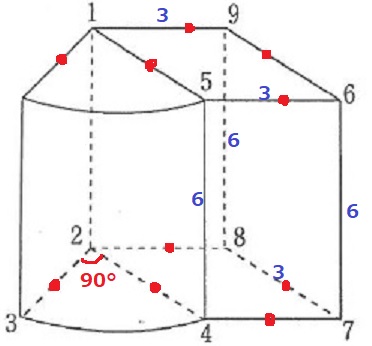
長さは正確に！
図では奥行きが高さと同じ長さのように見えるが３ｃｍです。
13.71＋６＋３＋６＋３＋６＋３
＝40.71ｃｍ（ア）
扇形の弧を通る３－４間が曲者なので、そこを避けるために後半の５－１間を狙う。
このとき、Ｐが通る５辺はどれも時間が等しいので、各辺を通過する時間は、
（16.71－9.21）÷５
＝7.5÷５＝1.5秒
イはアに近いので、イの値はアから引き算すればいい。
14秒後から、Ｐが９に到着するまでの時間は、
16.71－14－1.5＝1.21秒
８－９間でＰは1.5秒で６ｃｍ移動するので、
？＝６×1.21/1.5＝4.84ｃｍ
したがって、40.71－３－4.84＝32.87ｃｍ（イ）
ア…40.71、イ…32.87、ウ…13.71
難関中（算数科）解説ページに戻る
コメント