問題ＰＤＦ
下のように、ＡからＰまでに、ある整数が入っている表があります。
この表に、次の規則に従って〇か×の印をつけます。
①ＡからＰまでの数の１つに〇をつけ、
その数と同じ行、同じ列に並んでいる印のついていない数すべてに×をつける。
②印のついていない残りの数の１つに〇をつけ、
その数と同じ行、同じ列に並んでいる印のついていない数すべてに×をつける。
③もう一度②を行い、残った数に〇をつける。
この表では、どこを選んで〇をつけていっても、①から③の作業をした後に
〇をついた数の和がいつでも同じになることが分かりました。
〔 〕にあてはまる数を入れなさい。
（１）
①から③の作業をした後に〇をついた数は全部で〔 〕個あり、
それらの数の和はいつでも〔 〕です。
（２）
Ａに入っている数は〔 〕、Ｇに入っている数は〔 〕です。
（３）
この表に入っている一番大きい数は〔 〕、一番小さい数は〔 〕です。
＠解説＠
（１）
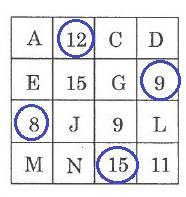
なぜ和が等しくなるのかはわからないが…
１行、１列ごとに〇が１つしかないように〇をつけると、〇の数は４個。
和は８＋12＋15＋９＝44
４・44
（２）
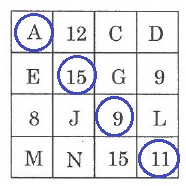
Ａを含むように〇をつける。
Ａ＝44－（15＋９＋11）＝９
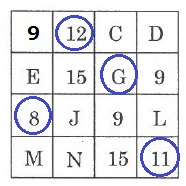
Ｇも同様。
Ｇ＝44－（８＋12＋11）＝13
９・13
（３）
残り７マスを埋めなくてはならない。
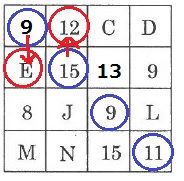
９＋15＋９＋11（青丸）において、
最初の９をＥに、15を12に変えても和が44になる。
ということは、９＋15＝Ｅ＋12
Ｅ＝９＋15－12＝12
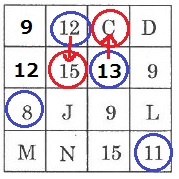
つづいて、12を15、13をＣに入れ替えると、
12＋13＝15＋Ｃ
Ｃ＝10
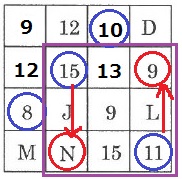
こんなこともできる。
15をＮ、11を９に変え、Ｎ＝15＋11－９＝17
正方形をつくり、その対角線上にあるペアの頂点を別のペアの頂点に入れ替えればいい。
（正方形は２×２、３×３、４×４のどれでもいい）
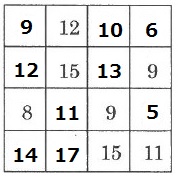
埋めていくとこうなる。
最大値は17、最小値は５。
17・５
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント