問題ＰＤＦ
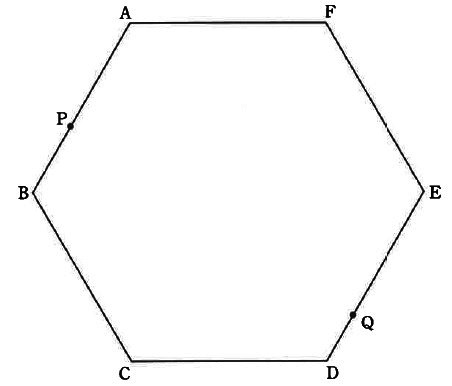
下の図のような、１辺の長さが２ｃｍの正六角形ＡＢＣＤＥＦがあります。
この正六角形の辺上を２点ＰとＱが移動します。
点Ｐは点Ａを出発して、毎秒２ｃｍの速さでＡ→Ｂ→Ｃと移動します。
また、点Ｑは点Ｄを出発して、毎秒１ｃｍの速さでＤ→Ｅと移動します。
このとき、次の問いに答えなさい。
（１）
２点Ｐ、Ｑが出発して１秒間は、直線ＡＤと直線ＰＱは常にある点Ｘで交わります。
点Ｘはどこにあるかを式やことばで説明しなさい。
（２）
２点Ｐ、Ｑが出発して１秒間で、正六角形ＡＢＣＤＥＦ内で直線ＰＱが通過した部分の面積は、
正六角形ＡＢＣＤＥＦの面積の何倍ですか。
（３）
２点Ｐ、Ｑが出発して1.5秒後のとき、四角形ＣＤＱＰの面積は
正六角形ＡＢＣＤＥＦの何倍ですか。
（４）
２点Ｐ、Ｑが出発して1.5秒後のとき、直線ＰＱと直線ＢＤの交点をＹとします。
このとき、ＢＹ：ＹＤを、最も簡単な整数の比で答えなさい。
＠解説＠
（１）
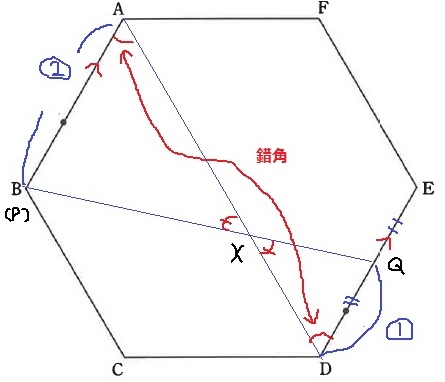
１秒後の様子を書いてみる。
ＢＡ//ＤＥ→錯角で∠ＸＡＰ＝∠ＸＤＱ
対頂角→△ＸＡＰ：△ＸＤＱ
この関係性はＰＱが移動中も変わらない。
ＡＸ：ＸＤ＝ＡＰ：ＤＱ＝２：１
答えは、『直線ＡＤを２:１に内分する点が点Ｘである』
（２）
先ほどの図で、△ＸＡＰと△ＸＤＱの和が正六角形の何分の何かを求める。
△ＸＤＱの面積比を①とおくと、△ＸＡＰ＝④
ＢＸ：ＸＱ＝２：１から、△ＢＤＸ＝②
四角形ＡＢＤＥは長方形で、ＡＤはその対角線。
△ＡＤＥ＝④＋②＝⑥
（四角形ＡＸＱＥ＝⑥－①＝⑤）
右の図のように考えると、四角形ＡＢＤＥ⑫は正六角形の２/３。
正六角形ＡＢＣＤＥＦは、⑫×３/２＝⑱
したがって、（④＋①）/⑱＝５/18倍
（３）
1.5秒後を図示。
ＰはＢＣの中点、ＱはＤＥを３：１に内分するところ。
ポイントはＢＣとＥＤを延長する。交点をＧとおく。
△ＣＧＤ＝④×④＝⑯
△ＰＧＱ＝⑥×⑦＝㊷
四角形ＣＤＱＰ＝㊷－⑯＝㉖
正六角形ＡＢＣＤＥＦ＝△ＣＧＤ×⑥＝⑯×６＝○96
よって、㉖/○96＝13/48倍
（４）
前問の四角形ＣＤＱＰの状態で、ＢＹ：ＹＤを求める。
線分を延長した交点をＧ、Ｈとする。
上も下も長さがわからないのがもどかしい(;￣Д￣)
ためしにＥＧ＝□とおいてみる。
△ＰＧＢと△ＰＨＣの相似比→１：１→ＨＣ＝⑧＋□
△ＱＨＤと△ＱＧＥの相似比→３：１
ここから、ＨＤ＝ＧＥ（□）×３と等式を作る。
⑧＋□＋④＝□×３
□×２＝⑫
□＝６
最後に、△ＹＧＢと△ＹＨＤの相似比から、
ＢＹ：ＹＤ＝ＢＧ：ＤＨ＝⑭：⑱＝７：９
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント