問題PDF
下の図のような直角三角形ABCでは、角(あ)の大きさが定まると3辺の長さの比が定まります。
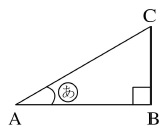
角(あ)との位置関係によって定まる2辺の長さの比の値について考えます。
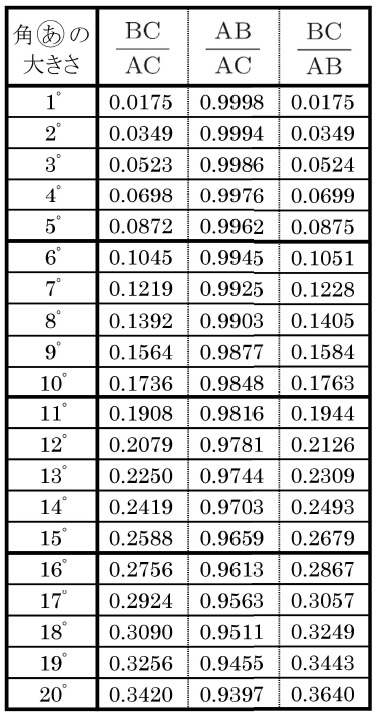
下の表は角(あ)が1°から20°までのときの、2辺の比の値を表したものです。
ただし、表の中の比の値は、小数第5位で四捨五入した値です。
たとえば、角(あ)が19°のときは
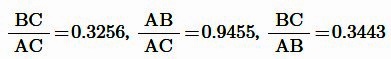
と定まります。
この表を利用して次の各問いに答えなさい。
ただし、問題文の中にある「光線」とは太さのないまっすぐ進む1本の光の線のことを表します。
また、壁の厚さについては考えないものとします。
(1)
図1は、AD=6.4m、BD=11.6mで、D地点には地面に垂直に立つ高さ1mの壁がある様子を表しています。今、B地点の真上にある位置Cから、壁に当たらないように壁の向こう側の地面に向けて光線を放ちます。
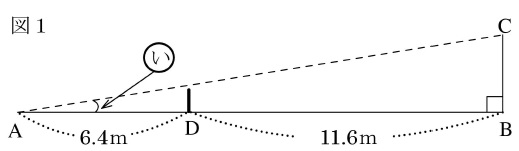
①位置Cが3mの高さにあるとき、次の問いに答えなさい。
(ⅰ)
位置Cから放たれた光線がA地点に届きました。光線は壁の上端の何m上を通過しましたか。
ただし、答えは小数で、小数第4位を四捨五入して小数第3位まで答えなさい。
(ⅱ)
位置Cから放つ光線が壁の向こう側の地面に届く位置を、光線を放つ向きを少しずつ変えながら、A地点からD地点に向かって近づけていきました。光線が届く壁の向こう側の地面の位置で最もD地点に近い位置は、D地点から何mかを答えなさい。
②位置Cから放たれた光線がA地点に届いたとき、光線と地面が作る角(い)が10°でした。光線が放たれた位置Cの地面からの高さは何mですか。ただし、答えは小数で、小数第4位を四捨五入して小数第3位まで答えなさい。
(2)
図2の四角形ABGFは地面の上にある長方形です。また、AD=6.4m、BD=11.6mで、AFとDEは平行で、DE上には地面に垂直に立つ高さ1mの壁があります。また、辺ABと対角線BFが作る角は13°です。B地点の真上にある地面からの高さが3mである位置Cから、壁に当たらないように壁の向こう側の地面に向けて光線を放ちます。
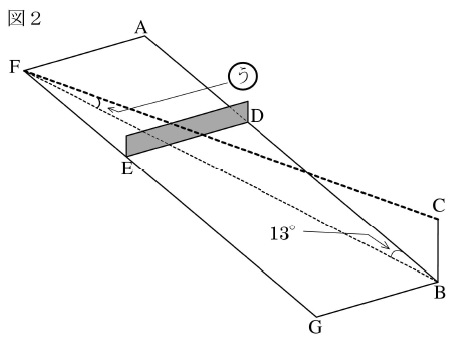
①地面の上にある長方形ADEF上で、光線が地面に届いた場所に色を塗りました。
色が塗られて部分の面積は何m2ですか。
ただし、答えは小数で、小数第4位を四捨五入して小数第3位まで答えなさい。
②長方形ABGF上の地点Fに光線が届いたとき、対角線BFと光線が作る角(う)は、
〔 〕°より大きい角度になります。〔 〕に当てはまる最も大きい整数を答えなさい。
@解説@
ドストレートに三角比(;^ω^)
小数第4位まで計算するので処理能力も要求される。
(1)①ⅰ
光線は1mの壁より上を通過する。
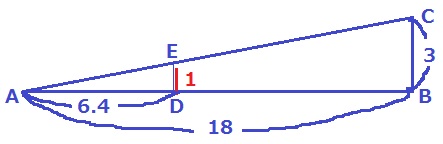
Dの真上でACとの交点をEとする。
△ABCと△ADEは相似。
DE=3×6.4/18=16/15
Eと壁上部の差は、16/15-1=1/15m=0.6666…→0.667m
ⅱ
光線をD側に寄せる→光線が壁の上部と接する。
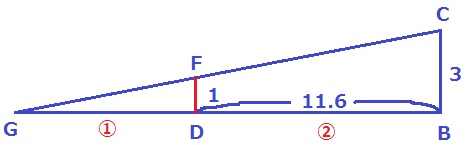
壁の上部をF、光線が地面に着いた地点をGとする。
DB=11.6mは変わっていない。
△CBGと△FDGの相似から、GD:DB=①:②
GD=11.6×1/2=5.8m
②
今度は、AD、DB間の長さを固定して、Cの高さを求める。

表から10°のとき、BC/AB=0.1763
AB=①とおくと、BC=〇0.1763
BC=18×0.1763=3.1734→3.173m
(2)①
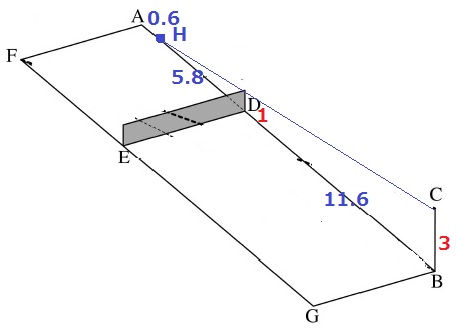
CからAに向けて光線を発射。地面に着いた点をHとする。
(1)①ⅱより、DH=5.8m
AH=6.4-5.8=0.6m
AHは光線が届く範囲。
ここから、光線を左方向に傾けるとどうなるか。

GFと光線が交わる点をIとする。
BHとBIの長さは異なるが、BC=3mと壁の1mは固定なので、
△HBCと△IBC内の三角形の相似から、光線上の比は①:②が維持される。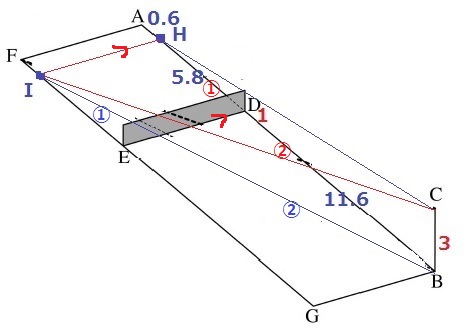
さらに、壁とBCが平行なので、平行線と線分の比よりHBとIBも①:②に内分される。
今度は、△BIHでとらえる。
HBとIBはEDとの交点でおのおの①:②に内分されるから、
三角形と比の定理の逆からIHと壁(ED)が平行。
つまり、四角形AHIFは長方形である。
AFの長さを求める。
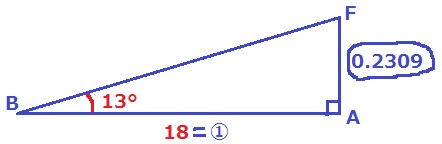
AF=18×0.2309=4.1562m
よって、四角形AHIFの面積は、4.1562×0.6=2.49372→2.494m2
②

(う)は△BCFの角度。
BC=3mなので残り2辺のいずれかの長さがわかれば、2辺の比の値から角度を調べられる。
BFは△ABFの辺。
つまり、△ABF内でBFを求め、△BCF内の2辺から(う)を求める。
FB=18×1/0.9744
(う)=BC/BF=3÷18/0.9744
=(3×0.9744)/18=0.1624
表の右列で0.1624は、9°(0.1584)と10°(0.1763)の間。
よって、(う)は9°より大きい角度になる。
@三角比@
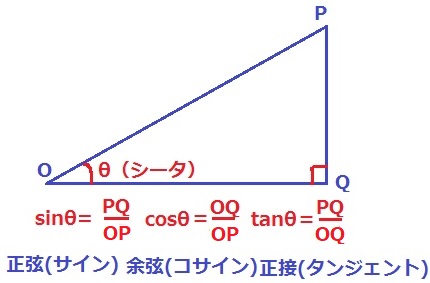
直角三角形の1鋭角をθ(シータ)とする。
このシータの値が決まると2辺の比の値が定まり、直角三角形の形が決まる。
◆正弦(sin;サイン)sinθ=PQ/OP
◆余弦(cos;コサイン)cosθ=OQ/OP
◆正接(tan;タンジェント)tanθ=PQ/OQ
詳しくは高校数学の数学Ⅰで習います。



コメント