問題ＰＤＦ
（１）
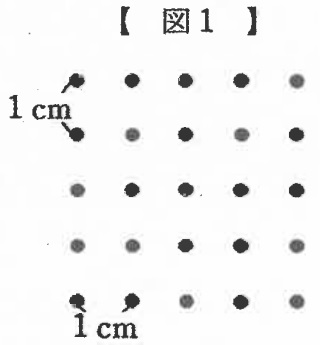
図１の点は面積が１ｃｍ2の正方形をすきまなく並べたときの頂点だけをかいたものです。
この点を結んで面積が10ｃｍ2の正方形を１つかきなさい。
（２）
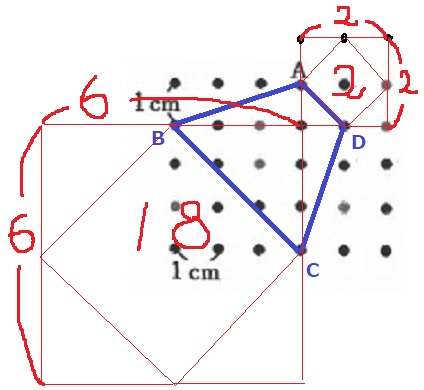
図２のように４つの正方形Ｐ、Ｑ、Ｒ、Ｓに囲まれた台形ＡＢＣＤがあります。
Ｐ、Ｑ，Ｒ、Ｓの面積はそれぞれ２ｃｍ2、10ｃｍ2、18ｃｍ2、10ｃｍ2です。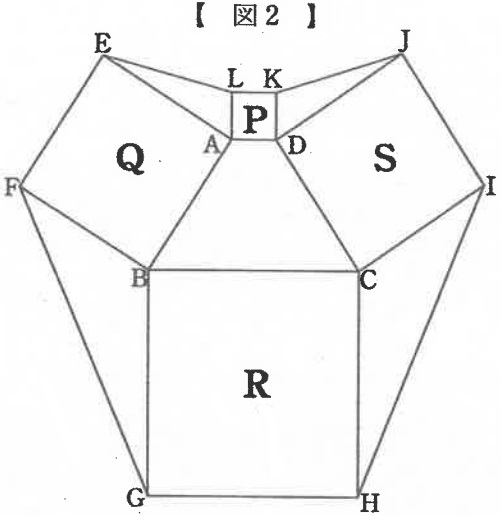
①
図３の点は面積が１ｃｍ2の正方形をすきまなく並べたときの頂点だけをかいたものです。
この点を結んで台形ＡＢＣＤを１つかきなさい。ただし、Ａは書いてある点を利用すること。
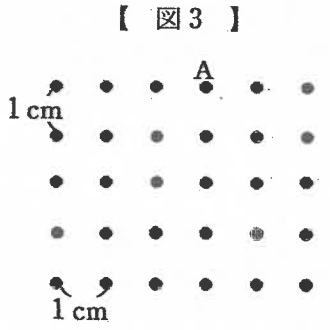
②
台形ＡＢＣＤの面積を求めなさい。
＠解説＠
根号つかいたい欲・・(›´ω`‹ )
（１）
面積が10ｃｍ2の正方形なので、１辺の長さは√10ｃｍ。
しかし、小学生は根号を習わないので、別の方法を探す。
10は平方数ではないので、線を縦か横でひいたらダメ。
ということは、斜めしかない。
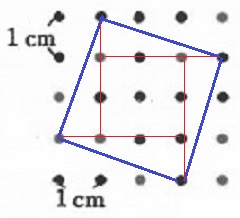
↑これが正解。
真ん中が２×２＝４ｃｍ2の正方形。
周りの直角三角形が３/２ｃｍ2で、４つだから６ｃｍ2。
和が10ｃｍ2となる。
全体が４×４＝16ｃｍ2なので、10/16ということは大きめにとらなければならない。
斜めの線で大きな正方形を作るように意識すれば、正答にたどりつけるはず。
*全体16ｃｍ2から、外側の６ｃｍ2を引く発想も可◎。
６は四方に分かれるので、３/２ｃｍ2の直角三角形になると目星をつけておく。
（２）①
前問より、10ｃｍ2の正方形の１辺は、１×４の長方形の対角線であった。
正方形Ｑが10ｃｍ2なので、まずＢの位置がわかる。
Ｂはなるべく左側にとらないと台形ＡＢＣＤが書けなくなるので、
Ａから下に１、左に４離れた点がＢ。
正方形Ｐは２ｃｍ2。正方形Ｒは18ｃｍ2。
どちらも２倍すると平方数になる。
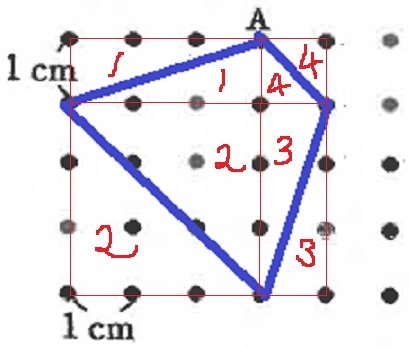
正方形の中に、面積が半分の正方形を作る。
２×２÷２＝２ｃｍ2、６×６÷２＝18ｃｍ2
２ｃｍ2の正方形の１辺は、１×１の対角線。
18ｃｍ2の正方形の１辺は、３×３の対角線。
ＡＤ//ＢＣとなり、ＣＤは１×４の長方形の対角線となる。
*正方形の中に面積が半分の正方形を描くという発想は、
半径がわからなくても、半径×半径さえわかれば円の面積が出せる問題でよく出てくる。
中学受験では頻出の発想なので、ぜひとも覚えておきたい。
②
前問のクリアが条件。
青い台形は、１辺４ｃｍの正方形の半分。
４×４÷２＝８ｃｍ2
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント