問題PDF
1とその数自身のほかに約数がない整数を素数といいます。
ただし、1は素数ではありません。
素数を小さい順に並べていくと、次のようになります。

異なる2つの素数の積となる数を『素積数』と呼ぶことにします。
例えば、2021=43×47となり、43も47も素数であることから、2021は『素積数』です。
素数は『素積数』でありません。
素数以外にも、次のような数は『素積数』ではありません。
・121(=11×11)や169(=13×13)のような、同じ素数の積となる数
・105(=3×5×7)や117(=3×3×13)のような、3つ以上の素数の積となる数
(1)
偶数の『素積数』のうち、小さい方から7番目の数を答えなさい。
連続する整数と『素積数』について考えます。
例えば、33、34、35…はすべて『素積数』です。
(2)
連続する4つの整数がすべて『素積数』であるということはありません。
その理由を説明しなさい。
(3)
100以下の整数のうち、連続する3つの整数がすべて『素積数』であるような組がいくつかあります。
上の例で挙げた33、34、35以外の組を、答え方にならってすべて答えなさい。
【答え方の例】(33、34、35)
(4)
連続する7つの整数のうち6つが『素積数』であるような組を、
答え方の例にならって1つ答えなさい。
【答え方の例】31~37の連続する7つの整数が答えの場合…(31~37)
@解説@
(1)
偶素数(偶数の素数)は2しかない。
奇素数(奇数の素数)の7番目は19だから、2×19=38
(2)
説明問題。
素数は基本的に奇数だが、偶素数2をかければ素積数は偶数となる。
→素積数の素因数2は最大で1個だけ。
連続する4つの整数には4の倍数があり、4の倍数は素因数2が2個ある。
4の倍数は素数積にならないので、連続する4つの整数すべてが素積数にはならない。
(3)
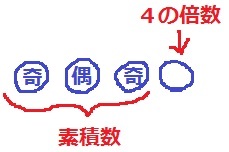
連続する4つの整数で4の倍数は素積数ではなかった。
ということは、連続する3つの素積数の並びは【奇数・偶数・奇数】となる。

2×(素数)=偶数の素積数を求め、その前後の奇数の素積数を1個ずつ調べていく。
2×3=6
前後の5と7は素数は素積数ではない×
2×5=10
9は素数の平方数で×。11も素数で×
2×7=14…13が素数で×
2×11=22…23が素数×
2×13=26…25は5の平方数×。27も×
2×17=34…例題と一緒で×!
2×19=38…37×
2×23=46…45と47×
2×29=58…59×
2×31=62…61と63×
2×37=74…73と75×
2×41=82…81と83×
2×43=86…85=5×17、87=3×29〇
2×47=94…93=3×31、95=5×19〇
これ以上は100を超してしまう。
したがって、(85、86、87)(93、94、95)
*問題文にのっている素数が登場したら、速やかに×と判断して迅速に調べる。
(4)
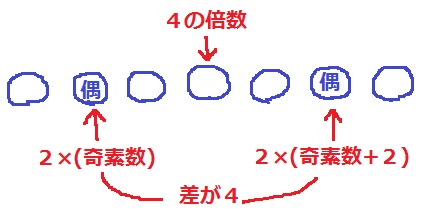
連続する7つの整数を詳しくみていく。
このうち6つが素積数なので、まんなかの4の倍数を境に左右3つが素積数となる。
本問も偶数の素積数に注目する。
この2つの差が4であるということは、2とかけ合わせる奇素数の差は2である。

前問の解答から、100以下の整数で題意を満たす組はなかった。
53以降の素数で差が2である組を探して、1つずつ調べていく。
(59、61)⇒(118、122)…117は9の倍数で×、121は11の平方数で×
(71、73)⇒(142、146)…147が49の倍数で×
(101、103)⇒(202、206)…207が9の倍数で×
(107、109)⇒(214、218)…213=3×71、215=5×43、217=7×31、219=3×73
したがって、(213~219)
@@
2つの素数の積で表される数(素数の平方数を含む)を半素数というそうです。



コメント