問題PDF
ボートを使って川下のA地点から川上のB地点に向かいます。ボートにはメインエンジンとサブエンジンがついていますが、メインエンジンのみでA地点からB地点に向かう予定でした。予定通りメインエンジンのみでA地点を出発したところ、出発して30分後にメインエンジンが故障して止まってしまいました。修理に25分かかった後、再びメインエンジンのみでB地点に向けて動き出したところ、予定より35分おくれてB地点に到着しました。もし、メインエンジンを修理せず、故障してすぐにサブエンジンのみに切りかえていれば、予定よりも25分おくれるだけですみました。また、サブエンジンのみでA地点からB地点まで向かえば予定よりも40分おくれて到着します。
このとき、次の問いに答えなさい。
(1) 得点率71.0%
川の流れの速さとメインエンジンのみで動かしたボートの静水時の速さの比を、
最も簡単な整数の比で答えなさい。
(2) 得点率17.9%
メインエンジンのみで動かしたボートとサブエンジンのみで動かしたボートの静水時の速さの比を、最も簡単な整数の比で答えなさい。なお、この問題は解答までの考え方を表す式や文章・図などを書きなさい。
(3) 得点率0.9%
はじめからメインエンジンとサブエンジンの両方を使用してA地点からB地点まで向かうとします。どちらのエンジンも故障しなかったとしたら、出発してから到着するまで何分かかりますか。
@解説@
(1)

メインエンジンだけなので、サブを除外してダイヤグラムを作成。
最初の30分間はメインを稼動、その後25分間は川に流される。
55分後からメインを再稼動、当初の速さと同じだから傾きは平行になる。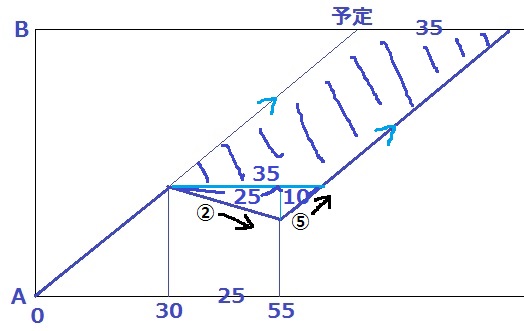
斜線の四角形は平行四辺形。対辺は等しく、35を下におろす。
流された距離にかかる時間の比は、25:10=5:2
速さは逆比で、流(川の流れ):上(上流に向かう速さ)=②:⑤
静水時の速さは、②+⑤=⑦
流:静=2:7
(2)

サブを追記。
30分後からサブだと予定より25分、最初からサブだと予定より40分遅れる。

平行線に注目して、三角形の相似を用いる。
25:15=⑤:③
③が30分だから、メインのみの到着予定時刻⑧は80分にあたる。
サブのみは、80+40=120分
時間の比は、メイン(上):サブ(上)=80:120=2:3
速さは逆比で、メイン(上):サブ(上)=3:2
前問の速さの比である〇に統一する。
メイン(上)が⑤なので、サブ(上)は⑤×2/3=〇10/3
サブ(静)は川の流れを足して、〇10/3+②=〇16/3
メイン(静):サブ(静)=⑦:〇16/3=21:16
*速さの比3:2はあくまで(上)の比であり、(静)ではない。
メイン(静)×2/3=⑦×2/3=〇14/3がサブの(静)にはならない!
一度、サブ(上)を経由して川の流れ②を足し、サブ(静)となる。
(3)
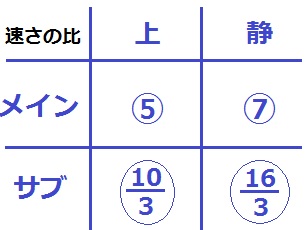
速さの比をまとめるとこうなる。
気をつけるべき点は、⑤+〇10/3=〇25/3にしないこと!
【上=静-流】だから、上+上だと-流を2つカウントする。
メイン+サブの(上)の速さは、⑦+〇16/3-②=〇31/3
(もしくは、⑤+〇10/3+②=〇31/3)
メインのみ(上):メイン+サブ(上)=⑤:〇31/3=⑮:㉛
時間は逆比で、メインのみ(上):メイン+サブ(上)=㉛:⑮
㉛が80分だから、80×⑮/㉛=1200/31分



コメント