問題ＰＤＦ
兄と弟は同時に学校を出発して、それぞれ一定の速さで家へ向かいました。
兄は1800歩あるいて家に着きましたが、急に雨が降ってきたため、
かさを持ってすぐに同じ速さで弟を迎えに行きました。
兄は200歩あるいたところで弟と出会い、その後、弟の速さに合わせて一緒に家に帰りました。
兄が弟を迎えに行ってから家に戻るまでに４分かかりました。
弟の歩数は１分間に９６歩であり、兄の歩幅は弟の歩幅よりも４ｃｍ長いです。
次の問いに答えなさい。
（１）
学校を出発したときの兄の速さは、弟の速さの何倍ですか。
（２）
兄は学校から家まで歩くのに何分かかりましたか。
（３）
兄の歩幅は何ｃｍですか。
＠解説＠
はじめは歩数で速さを考える。
（１）
弟は何歩で歩いたのかわからないので、兄の歩数のみで速さを捉える。
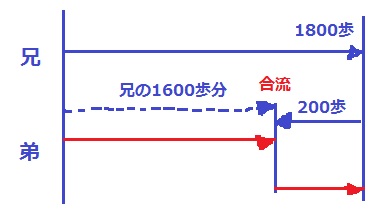
兄は行って戻って、弟と合流する。
同じ時間で兄は2000歩を歩いている。
弟が歩いた距離は、兄の歩数で考えると1800－200＝1600歩
兄：弟＝2000：1600＝5：４
よって、５/４倍。
（２）
時間は弟の迎えの４分しか情報がないので、そこに注目をする。
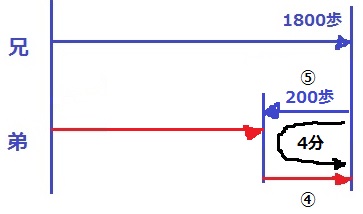
前問の速さの比を用いる。
兄が弟に会うまでは兄の速度⑤、弟に会ったあとは弟の速度④で歩く。
時間の比は速さの逆比。
兄200歩の時間は、４×４/９＝16/９分
兄は学校～家まで1800歩で行くから、
16/９×1800/200＝16分
（３）
長さの情報は『兄の歩幅は弟の歩幅よりも４ｃｍ長い』
速さ＝１分間の歩数×歩幅
前問より、兄は１６分で1800歩。
１分あたりの歩数は、1800÷16＝112.5歩
情報を整理して、歩幅の比を求める。
兄の歩幅…⑤÷112.5＝２/45
弟の歩幅…④÷96＝１/24
通分の要領で比を出す。
分子だけ抜きだすと、兄：弟＝㊽：㊺＝⑯：⑮
差の①が４ｃｍだから、兄の歩幅⑯は、
４×16＝64ｃｍ
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント