問題ＰＤＦ
下の図のように、半径４ｃｍの円があり、その周上に８つの点
Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ、Ｇ、Ｈが時計回りに等間隔に並んでいます。
次の問いに答えなさい。
（１）
三角形ＤＥＧの面積を求めなさい。
（２）
三角形ＢＤＧと三角形ＡＢＣの面積の差を求めなさい。
＠解説＠
（１）
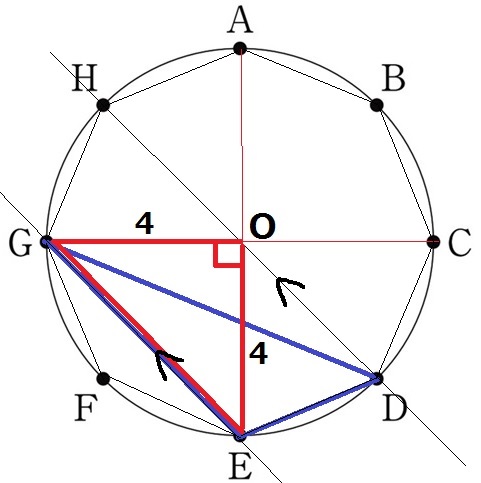
ＥＧとＤＨは平行。
ＤＨは正八角形の対角線で、この中心をＯとする。
△ＤＥＧを△ＯＥＧに等積変形すると、△ＯＥＧは直角二等辺三角形。
４×４÷２＝８ｃｍ2
＠＠＠
正八角形は等積変形をよく使うので、この平行線はおさえておこう。
（２）
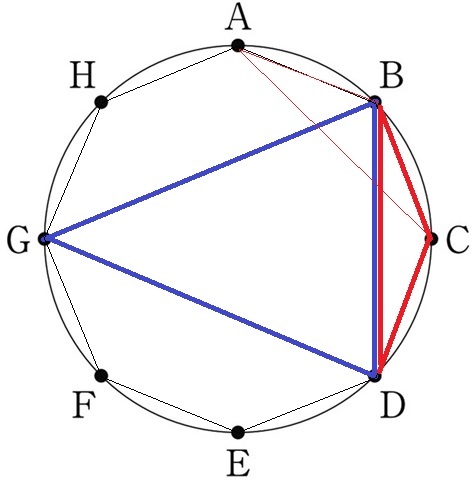
△ＡＢＣと△ＢＣＤは合同な二等辺三角形。
図形がかぶらない方が見やすいので、△ＢＤＧと△ＢＣＤの差を考える。
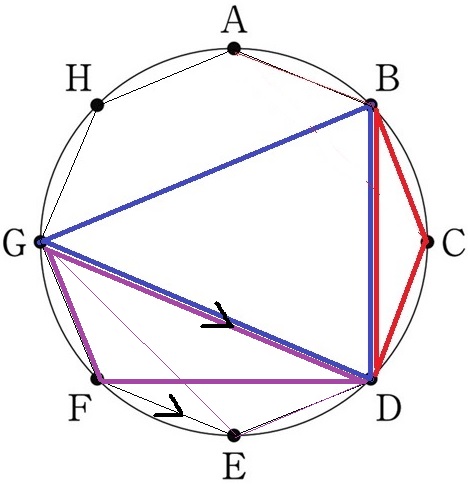
先ほどの△ＤＥＧ＝８ｃｍ2が使えないか。
ＤＧとＥＦが平行で、△ＤＦＧに等積変形してみる。
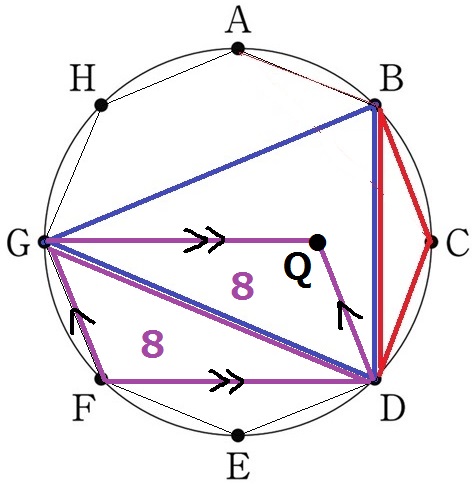
ＤＦとＦＧそれぞれに平行な線をひき、交点をＱとする。
四角形ＧＦＤＱは２組の対辺が平行だから平行四辺形であり、ＧＤは対角線。
△ＧＱＤは△ＤＦＧと合同で８ｃｍ2。
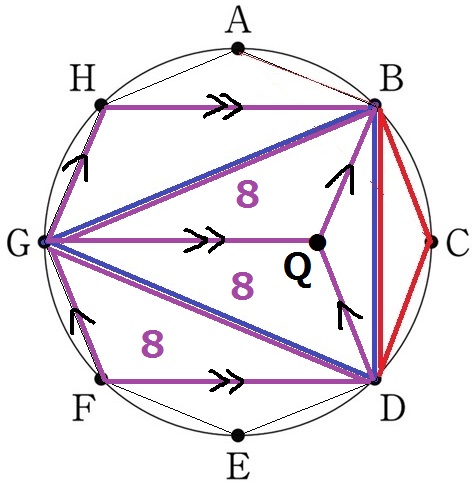
上も同じことをする。△ＧＱＢ＝８ｃｍ2。
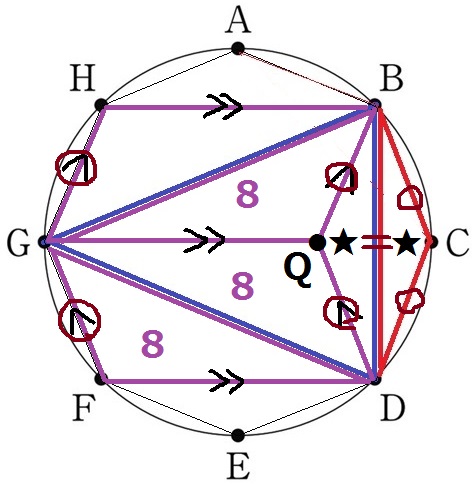
平行四辺形の対辺の長さは等しいので、〇はすべて長さが等しい。
ＢＤは共通辺。３辺が等しいから、△ＢＣＤと△ＢＱＤは合同。
△ＢＤＧと△ＢＣＤの差は、△ＧＱＤ＋△ＧＱＢ＝８＋８＝16ｃｍ2
＠別解＠
スチールさんから素晴らしい別解を頂きました。
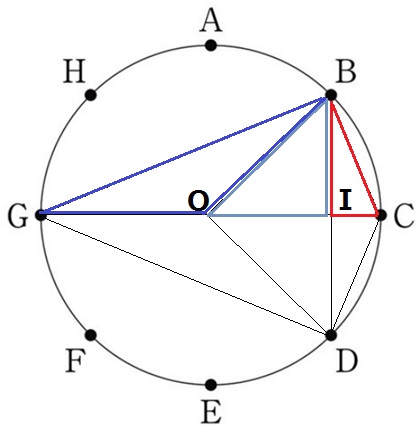
ＧＣとＢＤの交点をＩ、ＧＣの中点（円の中心）をＯとします。
まずは上半分の△ＢＯＧ（青）＋△ＢＩＯ（紫）と△ＢＣＩ（赤）の差を調べます。
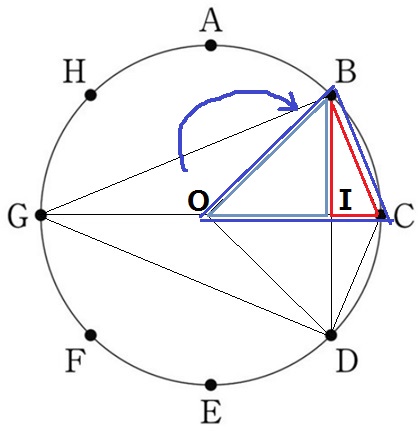
ＧＯ＝ＯＣより、△ＢＯＧと△ＢＣＯ（青）は等積です。
青＋紫－赤は紫が２枚分、すなわち、△ＯＢＩ２つ分です。
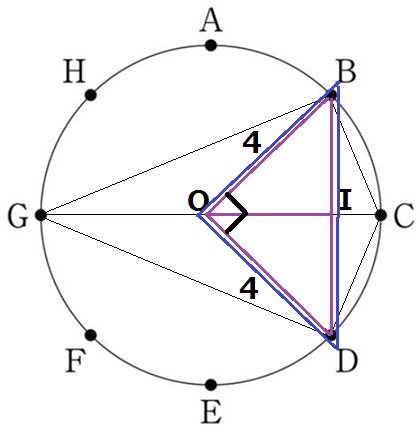
上下をあわせると、求めたい差は直角二等辺三角形ＯＢＤ２つ分です。
これは１辺が４ｃｍの正方形なので、４×４＝16ｃｍ2となります。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント