問題ＰＤＦ
家から公園まで一本道があり、その道のりは2160ｍです。兄と妹は、公園に向かって２人同時に家を出発しました。妹は公園に着くまでずっと歩き、兄は妹の歩く速さの３倍の速さで走りました。兄は公園に着いたらすぐ折り返して来た道を戻り、公園に向かっている妹に出会ったら、すぐ折り返して公園に向かい、これを繰り返しました。そして、兄は公園に３度目に着いた後、妹を待ちました。すると、兄が３度目に公園に着いてから、６分後に妹が公園に着きました。兄と妹はそれぞれ一定の速さで進み、折り返しにかかる時間は考えないものとして、次の問いに答えなさい。
（１）
兄と妹が１回目に出会った場所は、家から何ｍ離れていますか。
（２）
妹の歩く速さは分速何ｍですか。
＠解説＠
（１）
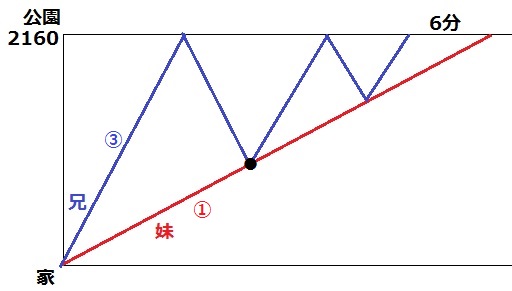
ヒストグラムを描くと、兄はギザギザになる。
公園で２度折り返して、妹と２回出会う。
１回目に兄と妹が出会った●に注目。
兄と妹の移動距離は合計で、2160×２＝4320ｍ
距離の比は速さの比。歩いた距離の比は、兄：妹＝③：①
家から●までは妹が歩いた距離だから、
4320×①/④＝1080ｍ
（２）
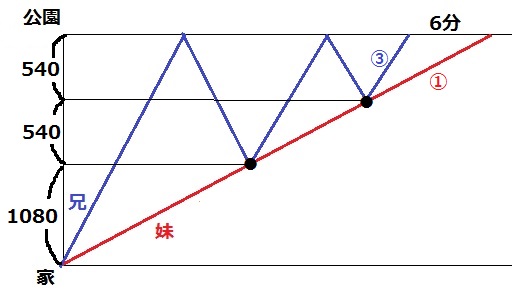
１回目に出会った場所は、ちょうど家と公園の真ん中だった。
兄の動きを見ると、公園に行ってから妹に出会うまでの形と同じ（相似）である。
つまり、２回目に出会う場所は後半の1080ｍの真ん中である。
⇒２回目に出会う場所は公園から540ｍ手前。
時間の比は速さの逆比。兄：妹＝【１】：【３】
最後の540ｍを兄は【１】、その６分後に妹が【３】の時間で歩く。
差の【２】が６分なので、妹の時間【３】は９分。
妹の速さは、540÷９＝分速60ｍ
難関中（算数科）解説ページに戻る
コメント