平均42.7点(前年比;-1.9点)
問題はこちら→東進ハイスクールさん(解答)
出題範囲の削減はなし。
大問1(小問集合)
(1)① 98.7%
3-7
=-4
② 92.0%
-1+4÷2/3
=-1+6
=5
③ 87.1%
3(2a+5b)-(a+2b)
=6a+15b-a-2b
=5a+13b
④ 86.0%
10/√2-√8
=5√2-2√2
=3√2
⑤ 74.5%
(x-2)(x+2)+(x-1)(x+4)
=x2-4+x2+3x-4
=2x2+3x-8
(2) 72.5%
x2+5x+3=0
解の公式を適用して、x=(-5±√13)/2
(3) 59.4%
4x+3y-8=0
3y=-4x+8
y=-4/3x+8/3
(4) 22.6%!
小数第1位が5になると、四捨五入で1つ上の整数になる。
13.5から14、14.5から15になる。
13.5≦a<14.5
(5)中央値…64.5%、最頻値…74.7%
10人の中央値(メジアン)は5番目と6番目の平均→21m
最頻値(モード)は最もあらわれている値で17m
大問2(小問集合2)
(1)① 27.5%!
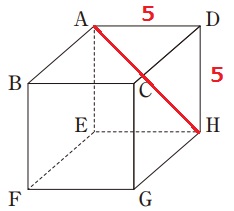
辺ABと垂直な面は、面AEHDと面BFGC
② 67.0%
ネジレ→延長しても交わらない、かつ平行ではない。
ADとネジレなのは、辺BF・CG・EF・HGの4本
③ 36.8%
直線GHと点Aとの距離を求める。
GH⊥面AEHD→AHは面AEHD上の線分なので、GH⊥AH
→AHを求めればいい。
△ADHは等辺5cmの直角二等辺三角形。
1:1:√2より、AH=5√2cm
(2)3点…38.6%、2点…12.0%、1点…23.3%

x>0で、xが増加するとyが減少するのは、
y=-x-2とy=-x2
ウ・エ
(3)① 55.7%
1か4を出せばいい。
2/4=1/2
② 19.7%!
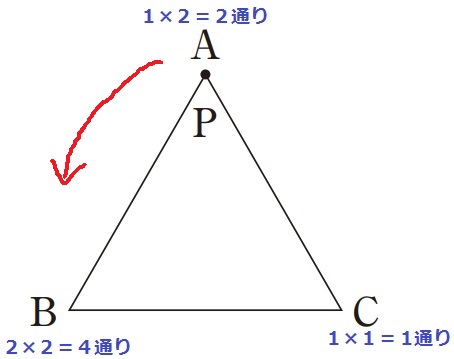
反時計回りに進めて1個先が2通り、それ以外が1通りずつある。
〔B⇒C〕は2×2=4通り
〔C⇒C〕は1×1=1通り
〔A⇒C〕は2回目にBを出せばCに移るので、1×2=2通り
計7通りで確率は7/16
(4)6点…20.6%!、5点…6.9%、4点…4.7%、3点…4.4%、2点…8.9%、1点…8.4%
答案では求める過程も記述する。
学校~家までの徒歩が分速80m、家~図書館の自転車が分速240m。
距離の合計は2000mで、時間の合計は18-5=13分
徒歩の時間をx分とすると、自転車は13-x分。
80x+240(13-x)=2000
160x=1120
x=7
午後4時7分に家に到着した。
家を出発した時刻はその5分後の午後4時12分
大問3(規則)
(1)①ア…94.2%、イ…90.9%

白は+2、+3…で増えていく。
黒は白よりワンテンポ遅れ、白の枚数-〇番目=黒の枚数
合計は平方数。
ア:15+6=21枚
イ:白の7番目と同じ。21+7=28枚
ア…21、イ…28
②4点…8.7%!!、3点…3.3%、2点…14.0%、1点…22.4%
ややこしく考えない
n番目の白をx枚とおく。
黒は問題文に書かれており、x-n枚。
合計はn番目の平方数でn2枚。
白+黒=合計
x+(x-n)=n2
2x=n2+n
x=(n2+n)/2
n番目の白の枚数は、(n2+n)/2枚

2018年埼玉大問3で、ほぼ同じ問題がでている。
(2)① 52.6%
4、10、16…と公差6の等差数列。
a+6=b
② 31.1%!
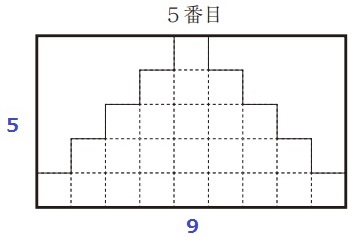
縦の長さはn番目のnと一緒。
横の長さは1、3、5…と奇数で増えていくので、n番目は2n-1。
50番目は縦50cm、横99cmの長方形。
(50+99)×2=298cm

2019年岐阜大問6で、似たような形の応用問題が出題されている。
大問4(数量変化)
(1) 65.4%
P:18÷3=6秒後
Q:6÷1=6秒後
P…6、Q…6
(2) 35.0%
1秒後はP(0、3)Q(1、0)
右に1、下に3さがるので傾きは-3
切片はPのy座標で3
y=-3x+3
(3) 2.2%!!
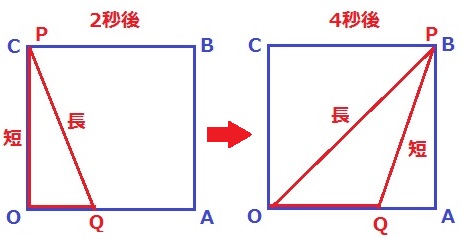
PがCに着く2秒後ではPO<PQだが、
PがBに着く4秒後ではPO>PQと逆転する。
ということは、PがCB上を移動しているときにPO=PQになる。
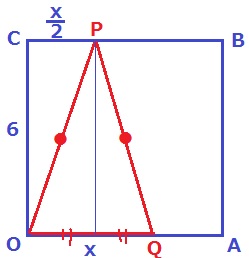
OQ=xとする。
△OPQは二等辺三角形で、頂角からおろした垂線は底辺を2等分する。
CP=x/2
Pの移動距離…6+x/2、Qの移動距離…x
PとQの速さの比は3:1。距離で等式を立てる。
6+x/2=3x
5/2x=6
x=12/5
12/5秒後
(4) 24.2%!
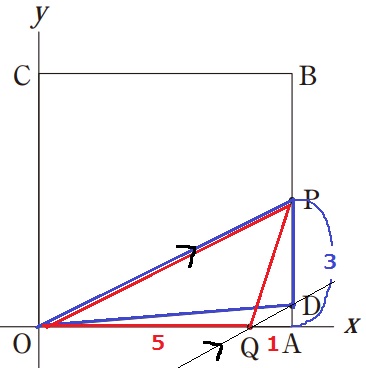
△OPQと△OPDの面積が等しいということは、
等積変形の要領でOP//QD
OQ=Qの移動距離=5
PA=(OC+CB+BA)-Pの移動距離=6×3-3×5=3
OPの傾きは3/6=1/2
QDの傾きも平行で1/2。
Qから右に1、上に1/2移動して、Dのy座標は1/2
D(6、1/2)
大問5(平面図形)
(1) 40.8%
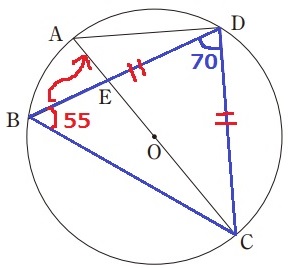
BCに補助線。
△BCDは二等辺ゆえ、∠DBC=(180-70)÷2=55°
弧CDに対する円周角で移す。∠CAD=55°
(2) 11.8%!
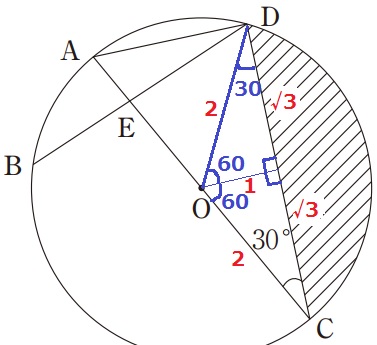
半径から△OCDは二等辺で、∠COD=120°
二等辺OCDを縦に割ると、辺の比が1:2:√3の直角三角形が見つかる。
△OCDの底辺CDは2√3cm、高さは1cm。
2×2×π×1/3-2√3×1÷2=4/3π-√3cm2
(3)6点…6.6%!!、5点…0.7%、4点…2.4%、3点…4.7%、2点…11.3%、1点…17.1%
AF=CDの証明。
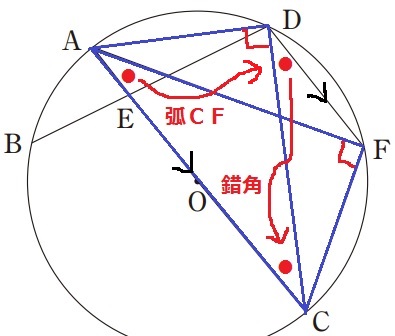
これらを1辺とする三角形に着目する。
△ACF≡△CADを指摘すればいい。
共通辺である直径AC。
半円の弧に対する円周角から、∠AFC=∠CDA=90°
弧CFに対する円周角と錯角で∠CAF=∠ACD
斜辺と1つの鋭角が等しい直角三角形で△ACF≡△CAD
対応する辺が等しく、AF=CDとなる。
(4)4点…1.6%!!、3点…0.2%
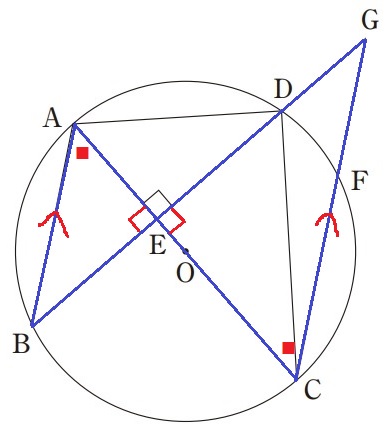
△ABEと△CGEは2角が等しく相似。
相似比さえわかれば面積比がでる。
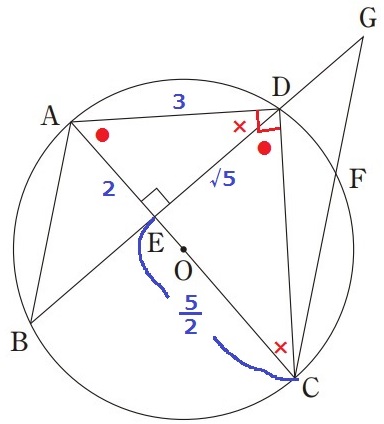
△ADEで三平方→AE=2cm
半円の弧に対する円周角で∠ADC=90°
直角三角形ACD・ADE・DCE内で●+×=90°の角度を調べると、
3つの直角三角形はすべて相似である。
AE:ED=DE:EC
2:√5=√5:EC
EC=√5×√5/2=5/2cm
△ABE∽△CGEにおいて、AEとCEが対応する辺。
AE:CE=2:5/2=4:5
面積比は相似比の2乗。△ABE:△CGE=16:25
●講評●
大問1
(4)算数でも似たようなものをやるが、正答率は良くない。
大問2
(2)すべて選べなので慎重な検討を要する。グラフを描いてみよう。
(3)②地味に条件がやらしい。
大問3
早々と規則をつかむこと。
(2)②長方形にしてしまう。
問題文のヒントなしでも発想できるようにしたい。
大問4
(3)Pのおよその位置に見当をつけたい。
POとPQの大小関係の変化に気をつける。
(4)等積変形⇒平行線
大問5
(2)扇形-△OCD。△OCDは有名角を利用。
(4)どの相似比で攻めるか。AC上にあるAE:CEの情報が得やすい。


コメント