問題ＰＤＦ
下の図のように平行四辺形ＡＢＣＤがあり、点Ｅは辺ＢＣ上の点、点Ｆは辺ＡＢ上の点、点Ｇは直線ＤＦと直線ＡＥの交わる点です。四角形ＡＥＣＤの面積が三角形ＡＢＥの面積の２倍で、四角形ＢＥＧＦと三角形ＢＤＦの面積が等しいとき、次の各問いに答えなさい。
（１）
ＡＧ：ＧＥを求めなさい。
（２）
三角形ＡＦＧの面積は、四角形ＡＢＣＤの面積の何倍ですか。
＠解説＠
（１）
四角形ＡＢＣＤは平行四辺形。
△ＡＢＥ：四角形ＡＥＣＤ＝ＢＥ：（ＡＤ＋ＥＣ）＝①：②
平行四辺形の対辺ＡＤ＋ＢＣの和が③
比を整数に統一するために和を⑥とすると、ＡＤ＝ＢＣ＝③
ＢＥ：ＥＣ＝②：①
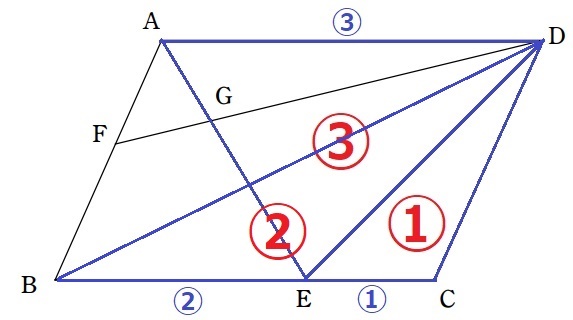
求めたいのはＡＧ：ＧＥ。
与えられた情報が面積だけなので、面積比でどうにかならないか。
ＤＥに補助線。
ＡＧ：ＧＥ＝△ＤＡＧ：△ＤＧＥ←これが知りたい。
△ＤＥＣの面積を①とすると、ＢＥ：ＥＣ＝②：①から△ＤＢＥ＝②
ＡＤ：ＥＣ＝③：①から△ＤＡＥ＝③
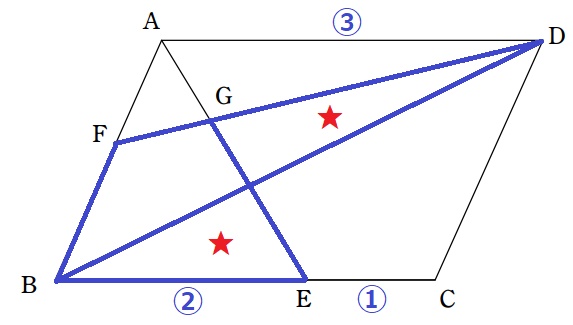
ここで、四角形ＢＥＧＦ＝△ＢＤＦを使う。
２つの図形から共通部分を抜いた★は等積である。
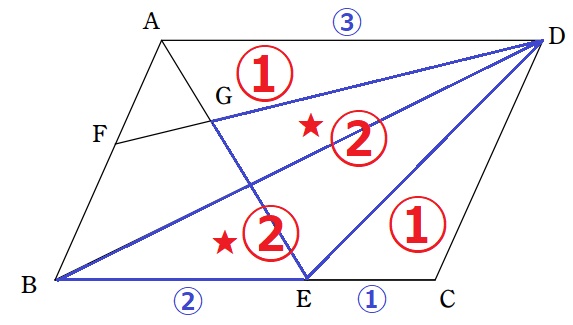
ということは、△ＤＢＥ＝△ＤＧＥ＝②
△ＤＡＧ＝③－②＝①
ＡＧ：ＧＥ＝△ＤＡＧ：△ＤＧＥ＝１：２
（２）
Ｆが絡む比が欲しい。
ＤＦとＣＢを外側延長、交点をＨとする。
△ＡＧＤ∽△ＥＧＨより、ＨＥ＝３×２＝６
ＨＢ＝６－２＝４
今度は△ＡＦＤ∽△ＢＦＨに注目して、ＡＦ：ＦＢ＝３：４
方針；【△ＡＢＣ→△ＡＢＥ→隣辺比で△ＡＦＧ】
１×１/２×２/３×（３×１）/（７×３）＝１/21倍
＠別解＠
等積の条件からＢＧとＥＤは平行、これを利用する解法を考えてみました。
ＡＧ：ＧＥ＝△ＡＢＧ：△ＧＢＥ＝①：②
ＢＥ：ＡＤ＝△ＡＢＥ：△ＡＥＤ＝③×３/２＝〇4.5
△ＡＧＤ＝〇4.5×１/３＝〇1.5
等積変形から△ＢＥＧ＝△ＢＤＧ＝②
ＡＦ：ＦＢ＝△ＡＧＤ：△ＢＧＤ＝３：４
ＦＧ：ＧＤ＝△ＡＢＧ：四角形ＡＧＢＤ＝２：７
△ＡＦＧの面積は、１×１/２×３/７×２/９＝１/21倍
難関中（算数科）解説ページに戻る
コメント