2019年度　フェリス女学院中学過去問【算数】大問３解説

問題ＰＤＦ
１辺の長さが31ｃｍの正方形の紙と、１辺の長さが23ｃｍの正方形の紙を、
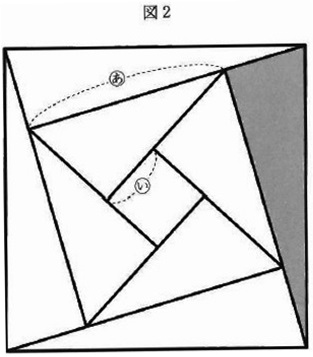
図１のように正方形に折ったものをそれぞれＡ、Ｂとします。
Ａの、紙が二重でない部分にＢをすき間なく重ねると、図２のようになりました。
色のついた部分の面積が84ｃｍ²のとき、次の問いに答えなさい。

（１）
（あ）の長さを求めなさい。

（２）
（い）の長さを求めなさい。

（１）
図１で考える。

折り返したところ全て84ｃｍ²
31×31－84×８＝289
289＝17×17
（あ）＝17ｃｍ

＠別解＠

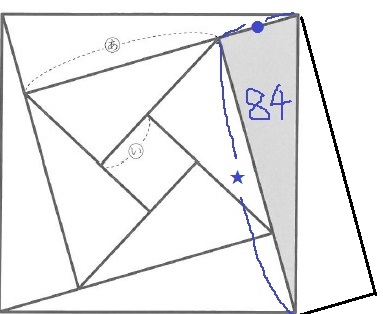
●×★＝84×２＝168
（●、★）＝（１、168）（２、84）（３、56）（４、42）
（６、28）（７、24）（８、21）（12、14）
●＋★は折り返す前の正方形の１辺である31ｃｍ。
７＋24＝31
（●、★）＝（７、24）
（あ）＝24－７＝17ｃｍ

（２）
ここも図１で考える。

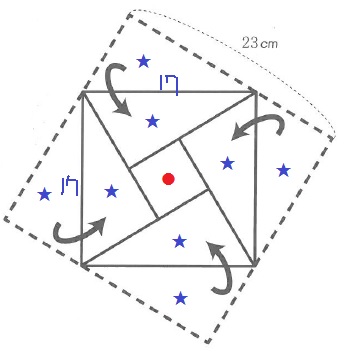
★は同じ。
17×17の正方形を２倍すると★８つと●２つ。
これから、23×23の正方形（★８つと●１つ）をひけば、
真ん中の正方形●の面積が求まる。
17×17×２－23×23＝49
49＝７×７
（い）＝７ｃｍ

＠＠
数学を使うのならば、三平方と２次方程式（中３レベル）で解けます。
（２）であれば、直角三角形の短い辺をｘとすると、他方の辺が（23－ｘ）
三平方の定理から、ｘ²＋（23－ｘ）²＝17²
２ｘ²－46ｘ＋240
＝ｘ²－23ｘ＋120＝（ｘ－８）（ｘ－15）＝０
ｘ＝８、15
長い辺が15、短い辺が８で15－８＝７
こちらの方が計算めんどいですね(;^ω^)
難関中（算数科）解説ページに戻る