問題ＰＤＦ
（７）
Ａ、Ｂ、Ｃ、Ｄ、Ｅの５人のテストの得点について、次のことがわかっています。
・Ａ、Ｂ、Ｃ、Ｄ、Ｅの５人の得点の平均は86点である。
・Ａ、Ｂの２人の得点の平均は、Ｄ、Ｅの２人の得点の平均より５点高い。
・Ｂ、Ｃの２人の得点の平均は、Ｄ、Ｅの２人の得点の平均より２点低い。
・Ｄの得点は、Ｃの得点より４点低い。
Ｃの得点が84点のとき、Ａ、Ｅの２人の得点の合計は何点ですか。
（８）
同じ大きさの立方体の積み木を積み上げて立体をつくりました。
下の図は、つくった立体を、真正面、真上の２つの方向から見たものです。
このように見える立体は、全部で何通りつくることができますか。
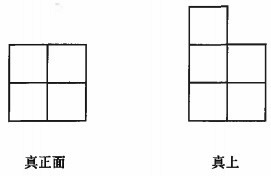
（９）
図１は、厚紙でつくられた立方体です。
この立方体を辺にそって切り開いたら、図２のようになりました。
図２のようになるには、立方体の辺をいくつ切ればよいですか。
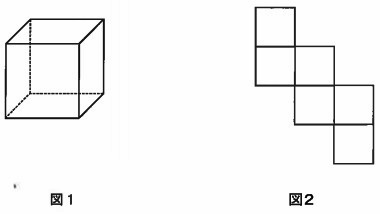
（10）
点Ｐを通り、三角形ＡＢＣの面積を２等分する直線を、解答用紙にかき入れなさい。
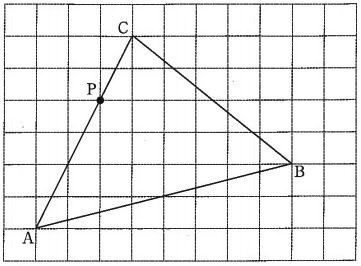
（11）
次の図は、２つを合わせると立方体ＡＢＣＤ－ＥＦＧＨになる立体を厚紙でつくったものです。
この立法の展開図において、四角形ＡＪＧＫと三角形ＪＦＧを表したものを選びなさい。
ただし、Ｊ、ＫはＢＦ、ＤＨの中点とします。
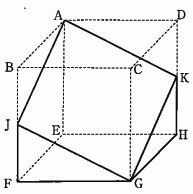
＠解説＠
（７）
Ｃ＝84点
Ｄ＝84－４＝80点
（Ａ＋Ｂ）÷２＝（Ｄ＋Ｅ）÷２＋５ ←すべて２倍
（Ａ＋Ｂ）＝（Ｄ＋Ｅ）＋10 …①
（Ｂ＋Ｃ）÷２＝（Ｄ＋Ｅ）÷２－２ ←同じく２倍
（Ｂ＋Ｃ）＝（Ｄ＋Ｅ）－４ …②
①、②から、（Ｄ＋Ｅ）を基準にすると、（Ａ＋Ｂ）が（Ｂ＋Ｃ）より14大きい。
（Ａ＋Ｂ）＝（Ｂ＋Ｃ）＋14
両辺からＢを除外。Ａ＝Ｃ＋14＝80＋14＝94点
Ａ～Ｅの平均が86点なので、
Ａ～Ｅの総和は86×５＝430点
430－（94＋84＋80）＝168 …Ｂ＋Ｅ
①より、（Ａ＋Ｂ）＝（Ｄ＋Ｅ）＋10
Ａ＝98、Ｄ＝80は、〔Ａ＝Ｄ＋18〕なので（右辺に＋18）、
上の式を成り立たせるには、〔Ｂ＋８＝Ｅ〕をする（左辺に＋８）。
つまり、ＢとＥの差は８で、Ｂ＜Ｅ。
ＢとＥの和差がわかったので線分図。
Ｂ＝（168－８）÷２＝80点
Ｅ＝80＋８＝88点
答えは、Ａ＋Ｅ＝98＋88＝186点
処理手順が多い。他に鮮やかな解法あるかな・・。
（８）
正面から見ると、左右ともに２段。
上からみた図で考える。
左は（１、１、１）がないから、２×２×２－１＝７通り
右は（１、１）の組合せがないので、２×２－１＝３通り
３×７＝21通り
（９）
図２の展開図で、切れていない辺（面同士がつながるところ）は５本。
立方体の辺は12本だから、切るべき辺は12－５＝７本。
今年の栄光学園で詳しい設問が出題されています。
立体から何本の辺を切れば平面に直せるか。一度は触れておきたいですね(*’ω’*)
（10）
Ｃを通り、ＰＢに平行な線をひき、ＡＢの延長線との交点をＣ’とおく。
ＣＣ’は下に１マス、左に３マスの傾きで下がるので、Ｃ’は２マス外にある。
△ＣＰＢと△Ｃ’ＰＢは等積変形で一緒。
ということは、△ＡＢＣ＝△ＡＣ’Ｐとなる。
ＡＣ’は横12マス分なので、ＡＣ’上で６マス目の点とＰを結んだ線が答え。
（11）
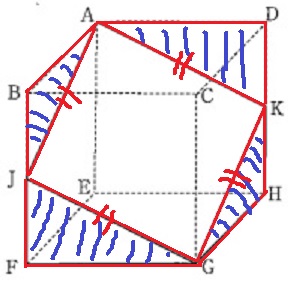
四角形ＡＪＧＫは、４つの合同な直角三角形の斜辺なので長さが等しい。
→四角形ＡＪＧＫは菱形。
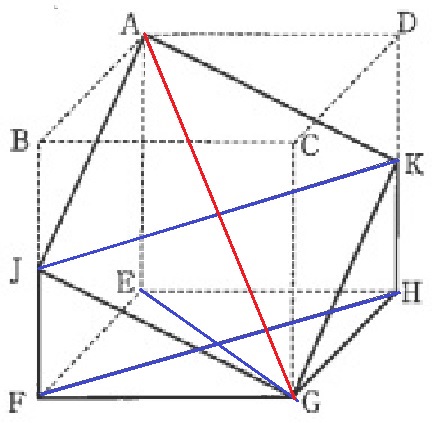
対角線ＡＧとＪＫの関係を考える。
ＪＫを平行に下にズラすと、底面の正方形ＥＦＧＨの対角線と同じ。
ＪＫ→ＦＨ→ＥＧと視点を変える。
ＡＧとＥＧを比較すると、ＡＧ＞ＥＧ。
よって、ＡＧ＞ＪＫとなるから、エ。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
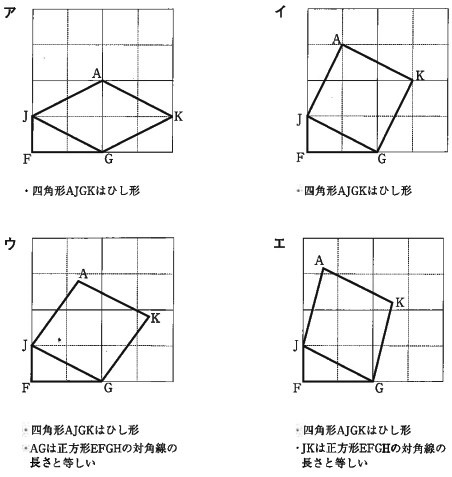
コメント