問題ＰＤＦ
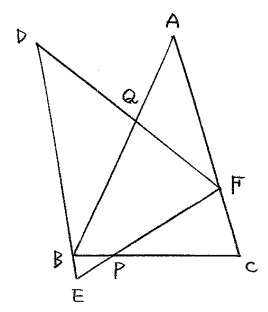
下の図の三角形ＡＢＣで、ＡＢ＝６ｃｍ、ＢＣ＝４ｃｍです。
辺ＢＣ上の点で、ＢＰ＝１ｃｍとなる点Ｐを中心として、三角形ＡＢＣを回転させると、
ＡはＤに、ＢはＥに、ＣはＦにうつって、Ｆは辺ＡＣ上、ＢはＤＥ上となりました。
辺ＡＢとＤＦの交点をＱとして、次の問に答えなさい。
（１）
ＡＦは何ｃｍですか。
（２）
ＡＱは何ｃｍですか。
（３）
三角形ＡＢＣと四角形ＢＥＦＱの面積比を最も簡単な整数の比で表しなさい。
＠解説＠
はじめの発想が肝心(;´･ω･)
（１）
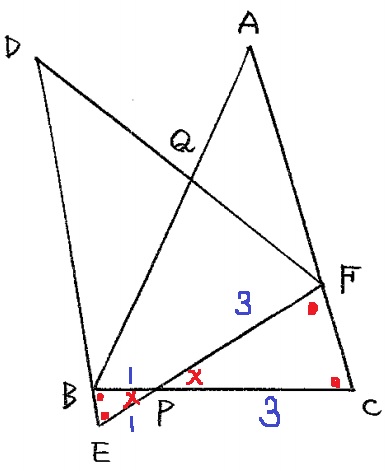
Ｐが回転の中心。
ＰＢ＝ＰＥ＝１ｃｍ、ＰＣ＝ＰＦ＝３ｃｍ
△ＰＢＥと△ＰＣＦは二等辺三角形となる。
対頂角から、∠ＢＰＥ＝∠ＣＰＦで、２辺の比とあいだの角度が等しくなり、
△ＰＢＥと△ＰＣＦは相似関係。
残りの４つの角度（●）はすべて等しい。
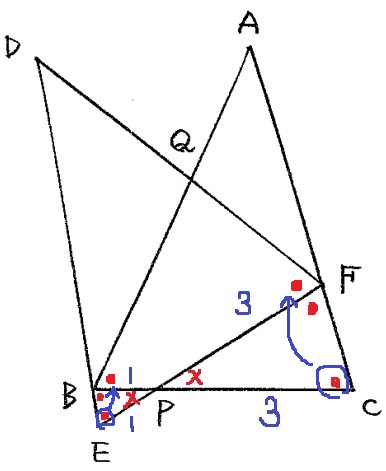
さらに回転移動から、∠ＡＣＢ＝∠ＤＦＥ＝●
∠ＡＢＣ＝∠ＤＥＦ＝●
…△ＡＢＣの底角がともに●で二等辺|дﾟ)
（ＡＢとＡＣの長さは違うように見えるが、作図が正確に描かれていない）
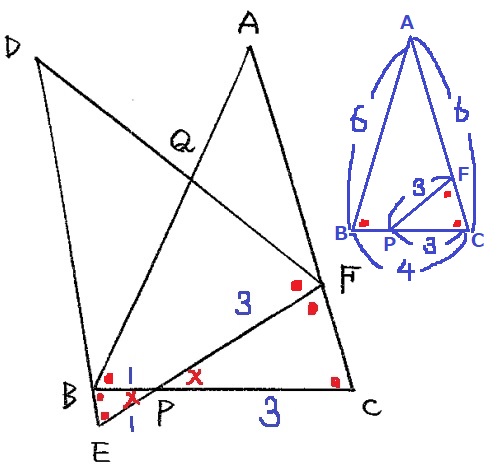
△ＡＢＣ∽△ＰＦＣに注目！
ＣＦ＝４×３/６＝２ｃｍ
ＡＦ＝６－２＝４ｃｍ
（２）
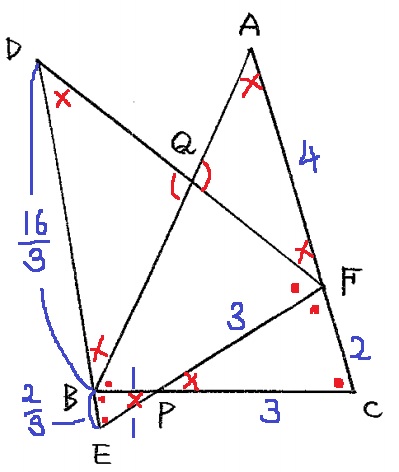
ＢＥ＝２×１/３＝２/３ｃｍ
ＤＢ＝６－２/３＝16/３ｃｍ
ニ等辺の内角は×－●－●なので、∠ＢＡＣ＝∠ＥＤＦ＝×
対頂角である∠ＡＱＦ＝∠ＤＱＢとあわせ、
２角相等より△ＡＱＦ∽△ＤＱＢ→∠ＡＦＱ＝∠ＤＢＱ＝×
（×＋●＋●＝180°と半直線からも、∠ＡＦＱ＝∠ＤＢＱ＝×を説明できる）
ＡＱ：ＤＱ＝ＡＦ：ＤＢ＝４：16/３＝③：④
△ＤＱＢは二等辺なのでＢＱ＝④→ＡＱ：ＱＢ＝③：④
ＡＱ＝６×３/７＝18/７ｃｍ
（３）
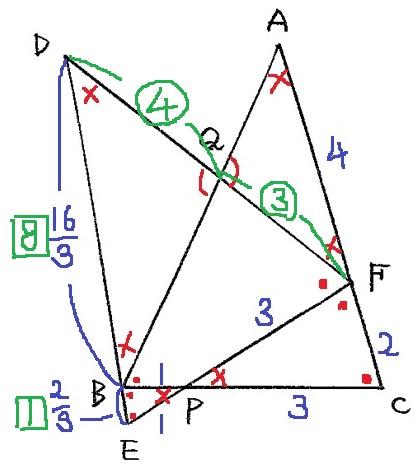
ＤＢ：ＢＥ＝16/３：２/３＝８：１
ＤＱ：ＡＱ＝４：３
△ＡＱＦが二等辺→ＱＡ＝ＱＦより、ＤＱ：ＱＦ＝４：３
△ＤＥＦ内部で面積比の計算。
△ＤＥＦ…９×７＝63
△ＤＢＱ＝８×４＝32
四角形ＢＥＦＱ＝63－32＝31
△ＤＥＦと△ＡＢＣは合同なので、
△ＡＢＣ：四角形ＢＥＦＱ＝63：31
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント