2021年度　西大和学園中学・県外過去問【算数】大問３解説

問題ＰＤＦ
大和君は、誕生日にロボットをプレゼントされました。
ロボットは下のような形をしていて、数字を表示する液晶盤Ａ、Ｂがついています。また、斜線の部分（以降「くちばし」と呼ぶことにします）がロボットの進む方向になっていて、ロボットは正方形のマスをつないだ板の上を動きます。

０から９までの数字のボタンやＡ、Ｂの２つのボタン、プログラム（Ⅰ、Ⅱ、Ⅲ）を選択できるボタンなどがついたコントローラーがあり、それを使ってロボットを動かすことができます。

Ａ、Ｂのボタンは直前までに押されたボタンの数字を液晶盤に表示するためのもので、リセットボタンはロボットのくちばしを北の方向に戻す役割を持っています。消去ボタンは液晶盤に表示されている数を消す役割を持ち、実行ボタンはプログラムに従ってロボットを動かす役割を持っています。また、ロボットは正方形の板の端まで進んだ場合、それ以上前へ進むことができず止まります。３つのプログラムは、表のような内容のものになっています。

ロボットを下の図の●の位置に、くちばしが北を向くように置くことを
「はじめの状態」とします。

ロボットを「はじめの状態」にし、
（例１）のように矢印の順でコントローラーのボタンを押しました。

すると、ロボットは次のような動き方をしました。

液晶盤Ａに18と表示され、液晶盤Ｂに７が表示され、
くちばしが東の方向に向くように向きを変え、３マス分進み止まる。

また、ロボットを「はじめの状態」にし、（例２）のようにコントローラーのボタンを押しました。すると、ロボットは次のような動き方をしました。

液晶盤Ａに35が表示され、液晶盤Ｂに８が表示され、くちばしが西の方向を向くように向きを変え２マス分進み、一度止まり、再び同じ方向に２マス分進み、くちばしが北の方向を向きとまる。
そして液晶盤Ａ、Ｂに表示された数字が消える。
つまり、ロボットははじめの位置から西の方向へ４マス進み、くちばしが北の方向を向いた状態で止まる。

次の問いに答えなさい。
（１）
大和君が「はじめの状態」にロボットをおき、以下のようなコントローラーのボタンを押してロボットを操作しました。ロボットが動いた後の状態を説明した文章の〔　　〕に入る適切な数字や語句を答えなさい。

【コントローラーの操作①】

ロボットの動いた後の状態
はじめの位置から〔　あ　〕の方向へ〔　い　〕マス進み、くちばしが〔　う　〕の方向を向いた状態で止まる。

（２）
大和君が「はじめの状態」にロボットをおき、コントローラーのボタンを押してロボットを操作したところ、ロボットは以下のように動きました。ロボットを動かしたときに押したボタンは以下の通りです。〔　　〕にあてはまると考えられる数字のボタンを答えなさい。

ロボットが動いた後の状態
はじめの位置から西の方向へ２マス、南の方向へ２マス進んだところで、くちばしが北の方向を向いた状態で止まる。
【コントローラーの操作②】

（３）
大和君が「はじめの状態」にロボットをおき、コントローラーのボタンを押してロボットを操作したところ、ロボットは以下のように動きました。ロボットを動かしたときに押したボタンは以下の通りです。〔　　〕にあてはまると考えられる数字のボタンを答えなさい。

ロボットが動いた後の状態
はじめの位置から東の方向へ３マス、北の方向へ１マス進んだところで、くちばしが東の方向を向いた状態で止まる。
【コントローラーの操作③】

（４）
下の図の斜線部分に障害物をおき、ロボットが通れないようにしました。大和君は、図の■印の位置でくちばしが西を向いた状態で止まっているロボットを、△印のところまでロボットを動かすためにコントローラーのボタンを押してロボットを操作しました。次の条件を満たすコントローラーのボタンの押し方を、例１や例２、コントローラーの操作①～③にならって答えなさい。ただし、ロボットは障害物にぶつかった場合は動かなくなるものとします。

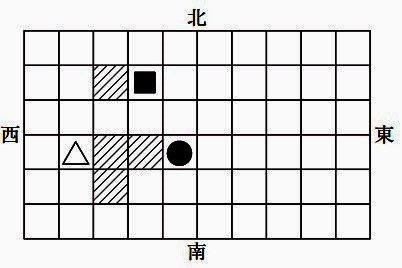
（条件）実行ボタンは３回だけ押す。

＠解説＠
（１）

↑条件整理
Ⅰは方向。東西南北ではなく、進行方向に対して回転する角度である点に注意！
Ⅱは進むマス。リセットでくちばしを北に戻す。板の端までいったら進めない。

Ｂに540が表示される。
Ⅱより、540の約数は10個以上（24個）あるので１マス進む。
Ａに７が表示される。
７÷４の余りは３だから西。

ロボットは西の方向へ１マス進む。
リセットは押さないので、くちばしは西を向いたまま止まる。
あ…西、い…１、う…西

（２）

Ａに【７□】が表示される。
西に進んだということは、７□÷４の余りは３である。
70～79のうち、４の倍数＋３は71か75か79。

Ⅲより、Ｂに【７□÷４の商】が表示される。
各々の商は、71÷４⇒17、75÷４⇒18、79÷４⇒19
２マス進んだから、約数が３～９個なので75と確定。
え…５
*２回目は西から反時計回りに90°回るので南へ進む。

（３）

空欄のない後半から考える。
Ａに【10】
リセットでくちばしは北を向いているので、10÷４の余りは２だから東。
Ｂに【７】
素数で約数は２個しかないから３マス進んだ。
ということは、『東へ３マス』は後半のプログラムであり、前半のプログラムは『北へ１マス』

Ａに【１□□】
北にいくので４の倍数＋１。
Ｂに【１□□÷４の商】
１マス進んだから約数は10個以上。

100～199を÷４すると、該当する商は25～49の範囲にある。
約数を多くするので、最小の素数２のベキ乗を考えてみよう。
次に小さい３を１個付け足すと…

48＝２×２×２×２×３（＝２⁴×３）
48の約数の個数は１（＝２⁰・３⁰）を含めて、
５（２⁰・２¹・２²・２³・２⁴）×２（３⁰・３¹）＝10個

Ａに入力された数は、48×４＋１＝193
お…９、か…３

（４）

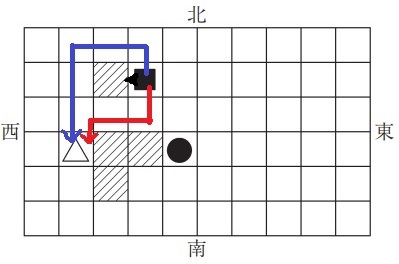
行き方は２通りしかない。
青ルート；北１→西２→南３
赤ルート；南１→西２→南１
初期状態はくちばしが西を向いていることに注意！

■解答例１

↑学校発表の解答例。

最初と曲がり角のたびにリセットでくちばしを北に戻す。
Ⅰの方向はＡ＝１～４で決めたほうがやりやすい。
１マス移動したい場合は前問の48を利用。

１回の命令文は、〔数字→Ａ→Ⅰ→数字→Ｂ→Ⅱ→実行〕
*〔数字→Ａ→数字→Ｂ→Ⅱ→Ⅰ〕でも良い。
次の命令文の前にリセットと消去（順序逆でもＯＫ）をはさんでクリアーな状態にする。
本番ではⅢは使わない方が無難。

■解答例２

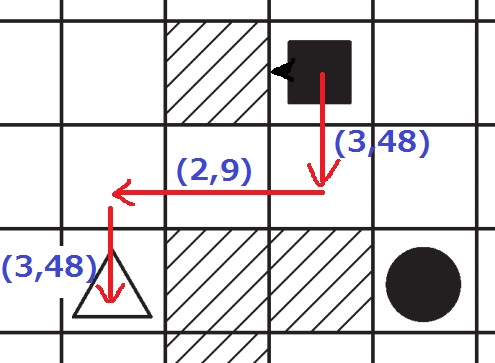
くちばしの向きに気をつければ、リセット無しでも行ける。

＠余談＠
『ロボットは障害物にぶつかった場合は動かなくなる』とありますが、
『ロボットは正方形の板の端まで進んだ場合、それ以上前へ進むことができず止まる』
ということは、後者の場合は次のプログラムを記述して実行すれば進めるはず？

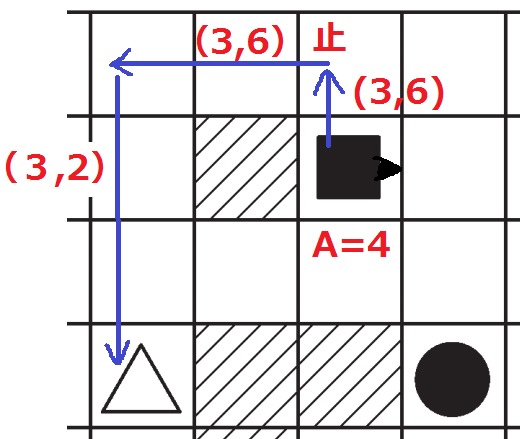
実行ボタンを４回使うのでダメなんですけど、
①最初にＡ＝４としてⅠだけ実行。くちばしを東に向ける。
②（Ａ、Ｂ）＝（３、６）とすると端で止まる。
③続けて同じ命令で実行ボタンを押すと進む（はず）。
④最後に（Ａ、Ｂ）＝（３、２）３マス進むにはＢに素数を入れる。

【４・Ａ・Ⅰ・実行・消去・３・Ａ・Ⅰ・６・Ｂ・Ⅱ・実行・Ⅰ・Ⅱ・実行・消去・３・Ａ・Ⅰ・２・Ｂ・Ⅱ・実行】でも行けそうかな？

最後に、2021年・高校生クイズ優勝おめでとうございます。
難関中（算数科）解説ページに戻る