問題PDF
次の〔 〕にあてはまる数を答えなさい。
(1)
ある店ではみかんを1個20円、りんごを1個80円、なしを1個90円で売っています。
この店で栄くんがみかんをりんごより3個多くなるように合計46個買ったところ、
代金は2570円でした。栄くんが買ったりんごは〔 〕個です。

(2)
次のような規則で分数が並んでいます。

73番目の分数は〔 〕です。
(3)
栄くんと東さんは学校を同時に出発して同じ道を通って駅に向かいました。栄くんは学校を出発した2分後に忘れ物をしたことに気付き、すぐに学校に向かって引き返したところ、30秒後に東さんとすれ違いました。栄くんは学校に到着した2分後に再び駅に向かって歩いて行ったところ、栄くんと東さんは同時に駅に到着しました。栄くんと東さんはつねに一定の速さで歩きました。東さんが学校を出発してから駅に到着するまでにかかった時間は〔 〕分です。
(4)
同じ高さまで水が入った2つの直方体の水そうがあります。2つの水そうの容積の比は9:32で、大きな水そうは小さな水そうの2倍の高さがあります。2つの水そうそれぞれに、さらに675mLずつ水を入れると、小さな水そうは全体の77%、大きな水そうは全体の28%まで水が入りました。大きな水そうにはじめから入っていた水の量は〔 〕mLです。
(5)
2022のように2種類の数字でつくられる4けたの整数は、2022も含めて〔 〕個あります。
(6)
下の図は、半径が1cmの円3つがすべて点Aを通るようにかいた図です。
太い線の長さは〔 〕cmです。

@解説@
(1)
『みかんをりんごより3個多くなるように買う』
→あらかじめ、みかん3個分をひくと、みかんとりんごの個数が同数になる。
残りの代金は、2570-20×3=2510円
残りの個数は、46-3=43個
みかんとりんごをまとめると、1セットあたり100円。なしは1個は90円。
合計代金2510円の十の位に注目する。
〇〇10円を作るには、なしの個数の1桁は9でなければならない。(90×9=810)
◆なし9個の場合
残りの代金は、2510-90×9=1700円
みかん&りんごのセットは、1700÷100=17セット
みかん17個、りんご17個、なし9個でちょうど43個になる。
よって、りんごは17個。
(2)
典型問題。

分母は1が1個、2が2個、3が3個…とつづく。
分子はグループごとの〇番目。
1~11の和は66だから、73番目は12グループ目で分母は12。
73-66=7番目
7/12
(3)

ダイヤグラムを描く。
『つねに一定の速さ』だから、栄が学校に戻ってくるのは4分後。
求めたいのは、東が駅に到着した時間。
栄と東の時間の比が知りたい…。

2人が出会う交点に注目する。
この距離を栄は4-2.5=1.5分、東は2.5分で進んでいる。
時間の比は、栄:東=1.5:2.5=③:⑤
栄は東の6分後に学校を出発して、同時に駅に到着した。
差の⑤-③=②が6分にあたるので、東が駅に到着したのは、
6×⑤/②=15分
(4)
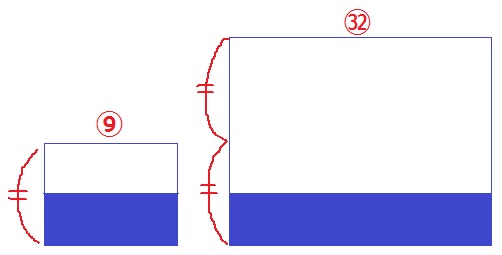
体積比が⑨:㉜で、高さが1:2。
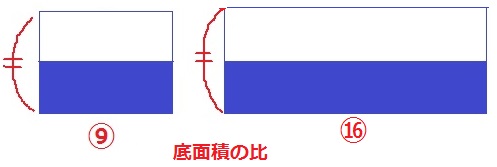
高さを統一して計算してみる。㉜→⑯
高さ共通なので、体積比は底面積の比になる。底面積の比は⑨:⑯

675mLを追加。
高さの比は底面積の比の逆比だから、この部分の高さは⑯:⑨
注意点は、大きな水槽は体積を半分にしたので、28%を2倍して56%にすること!
77-56=21%の差が⑦にあたる⇒3%が①
大きな水槽56%の体積は、675×①/⑨×56/3=25×56=25×(4×14)=1400mL
大きな水槽にはじめから入っていた量は、1400-675=725mL
(5)
最高位に0が使えないので、0を含むか含まないかで場合分けする。
◆0を含まない

2種類の数字をAかBとする。
数字の並びは各桁ごとで2通りずつ。これにAAAAとBBBBの2通りを引く。
2×2×2×2-2=14通り
AとBに入る数字の組み合わせは1~9から2つ選ぶ。
9C2=36通り
よって、14×36=504通り
◆0を含む
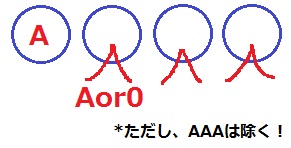
2種類の数字を0かAとする。
最高位はAが確定。残りはAor0。
3桁の並びはAAAを除いて、2×2×2-1=7通り
Aは1~9の9通りだから、9×7=63通り
したがって、504+63=567個
(6)
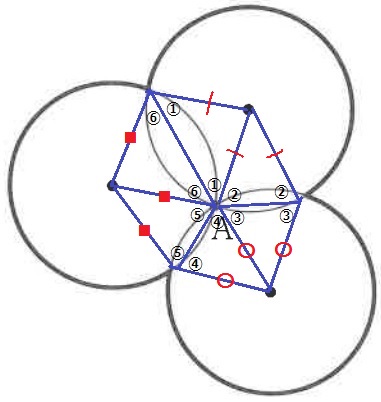
正六角形ではない点に注意。
二等辺三角形の底角に番号を付けてみると、
点Aの周辺部分より①~⑥の和が360°である。
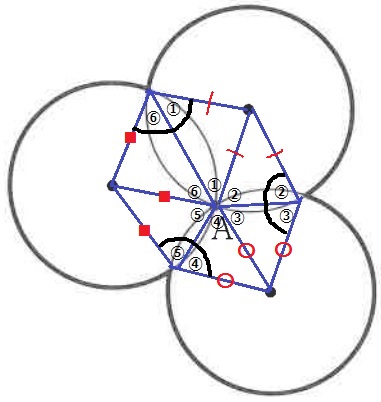
ということは、黒い部分で示した3つの角の和が360°
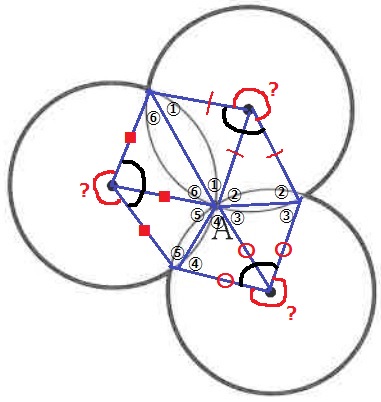
六角形の内角の和は720°だから、別の3つの角の和も360°
?の角の和は、360×3-360=360×2=720°
1×2×3.14×720/360=12.56cm



コメント