問題PDF
次の各問いに答えなさい。
(1)
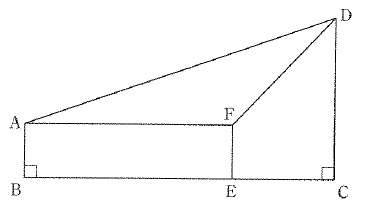
下の図は、面積の等しい長方形、三角形、台形を組み合わせできた台形ABCDです。
①DCの長さはABの長さの何倍ですか。
(2)
下の図1の直方体ABCD-EFGHを切ると、
図2のような体積の等しい3つの立体ア、イ、ウに分かれました。
AJ:JE=5:3、BK:KC=2:3であるとき、AIの長さはIDの長さは何倍ですか。
ただし、図2の立体ウは直方体です。

@解説@
(1)①
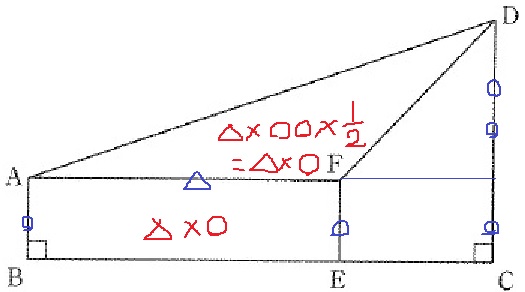
AF=△、AB=○とする。
長方形ABEFの面積は△×○
△AFDは底辺が△なので、高さが○○になれば面積が△×○になる。
CD=○○○
よって、DCはABの長さの3倍。
②

AB=①、DC=③
BC=□1とおく。
台形ABCDの面積は、(①+③)×□1÷2=△2
(○×□=△とする)
長方形ABEFは台形ABCDの3分の1なので面積は△2/3。
AFは、△2/3÷①=□2/3
AF:BC=□2/3:□1=2:3
よって、BCはAFの3/2倍。
(2)
1つの面が共通していれば辺の長さが体積比になるので、
共通する面を見つけ、直方体の体積比を考える。

AJ:JE=5:3より、直方体ウの体積を⑤とおくと、その下の直方体の体積は③となる。

1つのパーツの体積が⑤なので、イの奥の直方体は②となる。
BK:KC=2:3からアの奥が③となり、アの手前は②となる。
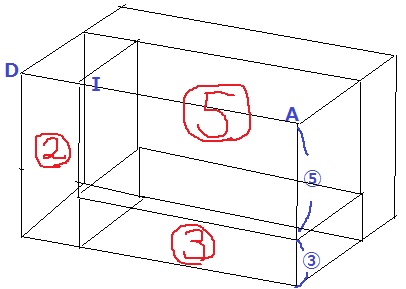
AI:ID=⑧:②=4:1
AIはIDの4倍。



コメント