2019年度　洗足学園中学過去問３回目【算数】大問３解説

問題ＰＤＦ
（１）　正解率83.7％
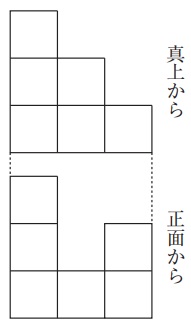
１辺の長さが１ｃｍの立方体をいくつか積み上げた立体を真上と正面から見たところ、下の図のように見えました。このような立体のうち、体積が最小のものは何ｃｍ³ですか。

（２）　正解率40.9％
Ａ町から3.5ｋｍ上流のＢ町までボートで川を上りました。出発してから15分間は一定の速さで進みましたが、15分後にエンジンが止まってしまいました。その後エンジンを直しましたが、出発の時より速さが遅くなりました。グラフはボートがＡ町を出発してからＢ町に着くまでの様子を表したものです。ボートが静水時に進む速さについて、エンジンが止まった後は止まる前の何％ですか。

（３）　正解率29.7％
縦12ｃｍ、横20ｃｍの長方形の紙がたくさんあります。これらの紙を出来るだけ枚数が少なくなるように同じ向きに貼り合わせて縦28ｃｍ、横150ｃｍの長方形をつくります。このとき、紙が２枚だけ重なっている部分の面積の合計は何ｃｍ²ですか。なお、この問題は解答までの考え方を表す式や文章・図などを書きなさい。

（４）　正解率9.3％
１から９までの９個の整数の中から数を選び、以下のように分数を作ります。

初めに４つの異なる数を選びそれらの積を分母、次に残りの５個の整数の中から４つの異なる数を選びそれらの積を分子とする。

作った分数をできるだけ約分した数をＡとします。
例えば、初めに１・３・７・８を選び、次に残りの５個の整数の中から２・５・６・９を選んだ場合、となります。
なお、この問題は解答まで考え方を表す式や文章・図などを書きなさい。

＠解答＠
（１）
体積が最小のものを答える。

真上から見た図に数字を書き込もう。
一番手前で正面から見える形をつくり、見えない後ろをすべて１にする。
９ｃｍ³
*ちなみに体積が最大だと13ｃｍ³になる。

（２）

情報整理力と処理能力が問われる。

エンジン停止前の上りの速さ…2000ｍ÷15分＝分速400/３ｍ
川の流れ…400ｍ÷12分＝分速100/３ｍ
エンジン停止前の静水時の速さ…400/３＋100/３＝分速500/３ｍ

エンジン停止後の上りの速さ…1900ｍ÷20分＝分速95ｍ
エンジン停止後の静水時の速さ…95＋100/３＝分速385/３ｍ

したがって、385/３÷500/３×100＝77％

（３）
長方形の紙を『枚数が少なくなるように』同じ向きに貼る。
まずは、長方形を横長か、それとも縦長に貼るか判定する。

◆横長に貼った場合
縦…28÷12＝２…４→３枚
横…150÷20＝７…10→８枚
３×８＝24枚

◆縦長に貼った場合
縦…28÷20＝１…８→２枚
横…150÷12＝12…６
→13枚
２×13＝26枚

よって、横長に貼ったことになる。
（*採点者所見によると、この点を調べていない答案がほとんどだったそう。
答えが当たっていても減点される危険もあるので、きちんと判定しておこう）

この後が大変:( ´ω` ):
２枚重なっているところを探す。

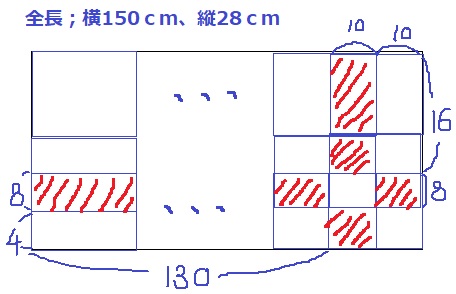
左上から下に向かうと、４ｃｍ分が余るので、その上の８ｃｍがダブる。
左上から右に向かうと、10ｃｍ分余るので、その左の10ｃｍがダブる。
このダブりは帯状につながるが、注意すべきは右下の長方形に４枚重なるところがある！
すると、２枚ダブるところは赤線のエリア。
長さを丁寧に認定して、８×（130＋10）＋10×（16＋４）＝1320ｃｍ²

＠別解＠
十字の交点の面積さえわかれば、全体から引いてもよし。
すなわち、12×20の長方形24枚分から全体の長方形28×150をひき、
さらに、４枚重なっている十字の交点10×８から３枚分を引く。
12×20×24－28×150－10×８×３＝1320ｃｍ²
こっちの方が面倒くさいか(´ㅂ`;)

＠追記＠

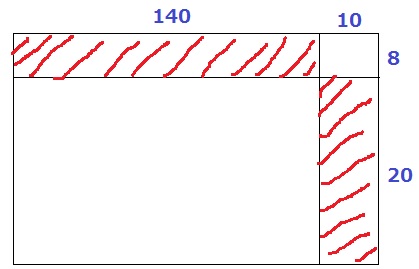
赤線を端っこに寄せ、クロスの部分を角に置くと計算しやすかった。
140×８＋20×10＝1320ｃｍ²

（４）
本試験で最も正解率が悪かった難問。

16＝２×２×２×２
分子に２の素因数を４つだけ残せば、分子が16になる。
２、４＝２×２、６＝２×３、８＝２×２×２
とりあえず、先に偶数を分子に配置してみよう。

分母に偶数を配置すると約分で２の素因数を減らせる。
分子の２の素因数４つを残すパターンは、この３つしかないと思われる。

ここから○に奇数を代入していく。
偶数の約分に配慮すること！

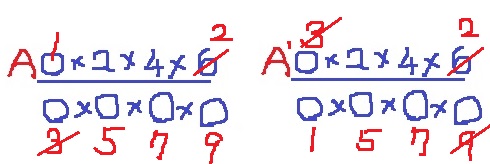
左上の○から考えよう。
ここは約分で１にしなくてはならない。
５つの奇数のなかで１にできるのは１か３のみ。
また、分子の６を３で約分して２にする必要がある。

分子に１を代入すると、分子は３・５・７・９となり、６を約分できる。
分子に３を代入すると、分子は１・５・７・９となり、３が約分で１となり、
同時に６も３で約分できる。
Ａの分母→５×７×９＝315　Ａ’の分母＝５×７＝35

分子の○２つに代入する奇数は、１・３・９しかない。
なぜなら、５・７は素数なので約分ができず、分子に残ってしまうから。
すると、うえの３つのパターンしかない。
Ｂの分母→３×５×７＝105　Ｃの分母→315　Ｃ’の分母→35
よって、答えは35・105・315。
*分子が16なので、分母に偶数は残らない。
ということは、分母に残る可能性のある数字は３・５・７・９のどれか。
２の素因数を４個にするためには、４つの奇数はすべて用いることになる。
５と７は素数ゆえ残る。３と９がともに分母に残らないとわかれば、
５×７ or ３×５×７ or ５×７×９となる。
難関中（算数科）解説ページに戻る