2019年度　ラ・サール中学過去問【算数】大問６解説

問題ＰＤＦ
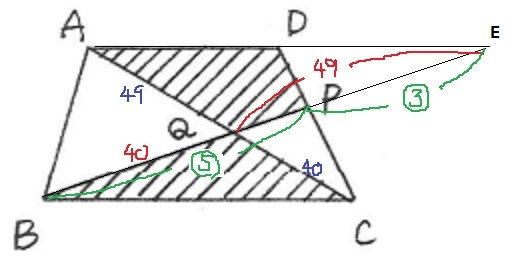
ＡＤ：ＢＣ＝５：８でＡＤとＢＣが平行な台形ＡＢＣＤにおいて、
辺ＣＤ上に点Ｐをとり、ＢＰとＡＣの交点をＱとします。
このとき、四角形ＡＱＰＤの面積と三角形ＢＣＱの面積が等しくなりました。
次の問に答えなさい。

（１）
ＣＰとＰＤの長さの比を最もかんたんな整数の比で答えなさい。

（２）
ＡＱとＱＣの長さの比を最もかんたんな整数の比で答えなさい。

（３）
三角形ＡＢＱと三角形ＣＰＱの面積の比を最もかんたんな整数の比で答えなさい。

斜線の部分が等しい⇒△ＡＣＤと△ＢＣＰの面積が等しい。
（それぞれに△ＰＱＣを足しても和は同じだから）

ＡＤとＢＣは平行、ＣＤ上で高さの比を捉えると、
△ＡＣＤ＝ＡＤ×ＤＣ、△ＢＣＰ＝ＢＣ×ＣＰ
ＡＤ×ＤＣ＝ＢＣ×ＣＰ
ＡＤ：ＢＣ＝５：８だから、
ＤＣ：ＣＰ＝８：５になれば、△ＡＣＤと△ＢＣＰの面積が等しくなる。
よって、ＣＰ：ＰＤ＝５：３

（２）
前問さえ乗り切れば、よくある手口。

交点をＥとして、△ＰＢＣと△ＰＥＤの相似から、
ＤＥ＝８×３/５＝24/５
△ＡＱＥと△ＣＱＢの相似から、
ＡＱ：ＱＣ＝５＋24/５：８＝49：40

（３）

ＢＱ：ＱＥ＝40：49、ＢＰ：ＰＥ＝５：３
ＢＥを89として、これを５：３に分ける。
ＢＰ＝89×５/８＝445/８
ＱＰ＝445/８－40＝125/８
ＢＱ：ＱＰ＝40：125/８＝64：25
△ＡＢＱ＝ＡＱ×ＢＱ、△ＣＰＱ＝ＱＰ×ＱＣより、
△ＡＢＱ：△ＣＰＱ＝49×64：40×25＝392：125
難関中（算数科）解説ページに戻る